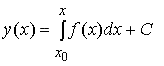Пусть f(x) — непрерывная на (a, b) функция и y(x) — ее первообразная . Тогда

y '(x) = f(x)

т.е. для отыскания первообразной получено дифференциальное уравнение 1-го порядка.

Решения этого уравнения известны:

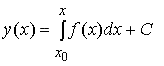
где С — произвольная постоянная, x ∈ (a, b), x₀ — некоторая точка из (a, b).

Чтобы выделить какое–то решение в задаче о вычислении первообразной , достаточно задать значение y(x) в какой–нибудь точке (a, b), например, y(x₀) = y₀.