| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Элементарная математика
а) Область определения: D (ctg x) = R \ {![]() n( n
n( n ![]() Z ) }.
Z ) }.
б) Множество значений: E (ctg x ) = R .
в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = ![]() .
.
д) Нули функции: ctg x = 0 при x = ![]() /2 +
/2 + ![]() n, n
n, n ![]() Z.
Z.
е) Промежутки знакопостоянства ;
![]() ;
; ![]() .
.
ж) Промежутки монотонности: функция убывает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
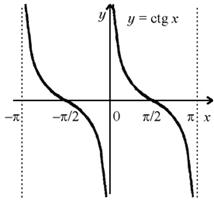
График функции y = ctg x изображен на рисунке.


 Тригонометрия
Тригонометрия Понятие угла в тригонометрии
Понятие угла в тригонометрии