Любое дифференциальное уравнение или система дифференциальных уравнений описывает с определенной степенью точности реальный физический процесс.

Приборы, фиксирующие то или иное физическое явление, не совершенны.

Может оказаться, что малая погрешность измерения начальных данных вызывает ”ощутимые” изменения решений уравнений. В этой ситуации нельзя гарантировать, что выбранная математическая модель реально отражает описываемое ею физическое явление.

И, наоборот, если малые возмущения начальных условий мало изменяют решения на всем промежутке их существования, то соответствующую математическую модель следует признать удачной.

Так возникает важный для приложений вопрос: при каких условиях, математическая модель, описываемая дифференциальными уравнениями, будет устойчивой.

Рассмотрим дифференциальное уравнение

Пусть некоторое фиксированное решение y = φ(x) этого уравнения существует при всех  x≥ x₀ .

Решение y = φ(x) уравнения называется устойчивым по Ляпунову при   x ≥ x₀ , если для любого ε > 0 существует число δ > 0 (зависящее, вообще говоря, от ε ) такое, что:

— решение y = y(x) задачи Коши с начальным условием y(x₀ ) , |y(x₀) − φ(x₀) | < δ , существует при всех  x ≥ x₀ ;

— для всех таких решений справедливо неравенство |y(x) − φ(x) | < ε , при всех   x > x₀ .

Геометрически это означает, что интегральные кривые y = y(x), близкие в момент x = x₀ к интегральной кривой y = φ(x), остаются близкими к ней и на всем промежутке [x₀, ∞) .

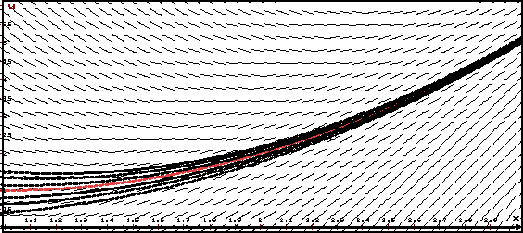
На рисунке красным изображено устойчивое решение задачи Коши y' = − y, y(1) = 1.

Видно, что все интегральные кривые, близкие к этому решению в начальный момент x = 1, остаются вблизи него и при x > 1 .

Решение y = φ(x) называется неустойчивым по Ляпунову при   x ≥ x₀ , если существует число ε > 0 такое, что для любого δ > 0

найдутся решения y = y_δ(x) и значение x₁ = x₁(δ) > x₀ такие, что хотя | y_δ( x₀) − φ( x₀) | < δ , но |y( x₁) − φ( x₁) | ≥ ε .

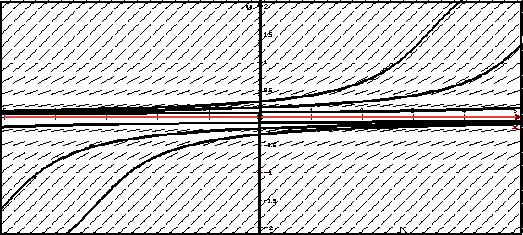
На рисунке красным изображено неустойчивое решение y = 0 задачи Коши y' = sin² y, y(0) = 0.

Видно, что интегральные кривые, близкие к   y = 0 в начальный момент x₀ = 0,   удаляются от  y = 0 с ростом x > 1 .