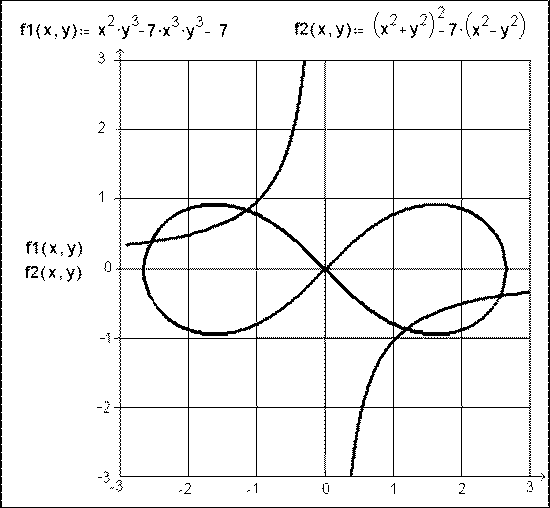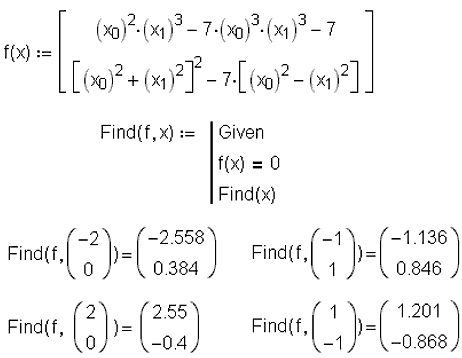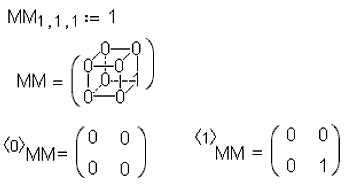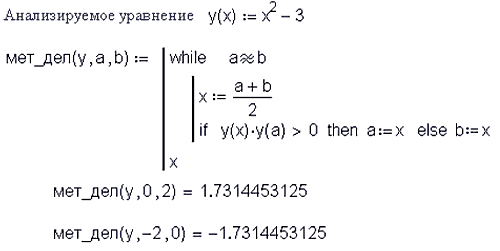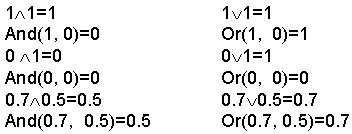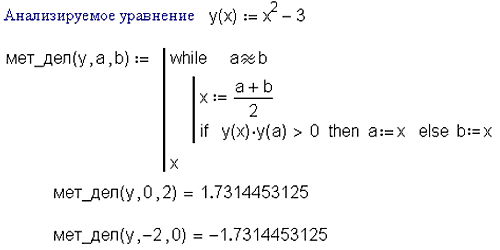Mathcad MM: новая программа – новые возможности(КомпьютерПресс, № 12, 1999)В.Ф. Очков http://twt.mpei.ac.ru/ochkov К.А. Орлов
Mathcad MM: новая программа – новые возможности 1. Декартов график неявной функции 2. Новая база операторов интерфейса 8. Древовидный оператор с более чем двумя ветвями операндов 9. Древовидные встроенные операторы 12. Структурирование Mathcad-документа 15. Расширенный оператор вывода 16. Группировка данных в запись 17. Решение задачи линейного целочисленного и дискретного программирования 18. Альтернативные математические операторы 21. Псевдоним переменной, функции и оператора 24. Системные переменные по параметрам атмосферы и пользователя 124. Связь между переменными (Variables Links) (Mathcad) 125. Более точное комментирование символьных преобразований 127. Функция RND работает и с массивом (RND-function works with array too) ПрологВ конце 1999 года фирма MatSoft, Inc. (http://www.matsoft.com) выпустила новую редакцию популярнейшей математической программы Mathcad. При этом были учтены замечания не только по ее содержанию, но и по ее названию. Дело в том, что приставка «2000», мягко говоря, не отличается особой оригинальностью[1]. В 1999 году на компьютерный рынок «как из мешка» были «высыпаны» программы с двойкой и тремя нулями – Windows 2000, Office 2000, Mathcad 2000, AutoCAD 2000, ТВТ Shell 2000 и т.д. и т.п. Приставка «ММ» в имени новой версии Mathcad – это, во-первых, римский (завуалированный) вариант вышеописанного арабского числа 2000. Во-вторых, «ММ» можно рассматривать как аббревиатуру таких «рекламных» фраз: «More Mathematic» («Больше Математики») или «Modern Mathematic» («Современная Математика») и т.д. Итак, что нового есть в среде Mathcad MM. 1. Декартов график неявной функцииПользователи Mathcad уже привыкли к тому, что новые версии этой программы всегда имеют новые возможности для работы с графикой. Mathcad MM — не исключение; в нем появилась возможность строить декартовы графики неявных функций. Основной недостаток декартового графика Mathcad и других подобных математических пакетов (MatLab, Maple, Mathematica и др.) состоит в том, что уравнение кривой должно быть записано в явном виде y(x)=... Но иногда бывает необходимо графически отобразить кривую, записанную в общем виде: f(y, x)=0. В старых версиях Mathcad для решения данной задачи приходилось вручную или средствами символьной математики решать относительно переменной y уравнение вида f(y, x)=0 и только потом строить график (несколько графиков, если решений несколько). Но, как должен понимать читатель, далеко не всякое уравнение можно решить аналитически. В среде Mathcad MM у оси абсцисс декартова графика можно записать не только функции y1(x), y2(x) и т.д., но и такое выражение – f(y, x). После этого будет построена нужная кривая. Разброс графика по оси x и оси y задается пользователем.
На рис. 1 показано графическое решение системы двух нелинейных алгебраических уравнений через новые возможности декартова графика Mathcad MM. Наша система (вторая кривая – это знаменитая лемниската Бернулли) имеет 24 корня, из которых четыре действительных[2]: они видны на пересечении кривых на рис. 1. 2. Новая база операторов интерфейсаВ среде Mathcad оператор «:=» является основным, поддерживающим интерфейс пользователя с этой математической программой. С его помощью переменным присваиваются числовые значения и определяются функции пользователя: А := 20, y(x) := х2 и т.д. Этот же оператор имеет аналогичное написание и действие в среде языка Pascal[3]. В других языках программирования (BASIC, например) пользовательские переменные и функции «рождаются» и обновляются с помощью оператора «=»: А = 20, y(x) = x^2 и т.д. В среде Mathcad оператор «=» является как бы антонимом оператора «:=» – оператор «=» предназначен не для ввода, а для вывода численного значения переменной, выражения, функции. Язык Pascal все больше и больше теряет свои позиции, уступая лидерство языкам С и BASIC[4]. Вследствие этого оператор «:=» становился неким анахронизмом – его нужно заменить на более привычный оператор «=». Но он в среде Mathcad, как уже отмечено выше, с самого начала был «мобилизован» на выполнение противоположной операции не на ввод, а на вывод численного значения переменной. Фирма MathSoft пытается разрешить это противоречие. Так, начиная с Mathcad 7, операторы «:=» и «=» несколько «перемешались» благодаря так называемой технологии SmartOperator («сообразительный» оператор). При вводе значения переменной теперь следует набирать на клавиатуре не «А:» (символ «=» система припечатывает сама), а «А=». Если переменная А что-то уже хранит, то это «что-то» (встроенное или пользовательское значение) выводится на дисплей: А = 20[5]. Если же переменная А свободна, то на дисплее появляется заготовка оператора «загрузки» переменной: А := ■. Черный квадрат (placeholder – «держатель места») пользователь заполняет выражением, содержащим константы, а также переменные и функции, видимые в данном месте Mathcad-документа[6]. Кроме оператора «:=» в среде Mathcad есть и два других, аналогичных по действию, но различающихся, если так можно выразиться, по радиусу действия. Оператор «º» (Triple equal – тройное «равно») делает пользовательскую переменную или функцию видимой во всем Mathcad-документе (оператор «:=» делает переменную и функцию видимой только ниже и правее места ее создания), а операто𠫬» (Left Arrow – левая стрелка) – внутри программного блока (см. пункт 6). Эти три оператора ввода позволяют создавать глобальные «º», полуглобальные (или полулокальные) «:=» и локальные «¬» переменные. У оператора «=» тоже есть «помощник» – оператор вывода аналитического (символьного) значения переменной или функции «®» (Right Arrow – правая стрелка). С появлением 2000-й версии «все смешалось в доме Mathcad». Теперь пользователь вправе менять в выражениях написание основных интерфейсных операторов по следующей схеме:
Пользователи Mathcad 2000 получили прекрасную «возможность» писать такие «ребусы»: А = 1 A = 1 A = 1 Здесь первый оператор – это оператор присваивания (локального, полуглобального или глобального – догадайся сам!), второй – вывод численного значения переменной, а третий – оператор сравнения переменной с единицей. «Who is who» можно понять, только подведя курсор к выражению. Это действие заставит операторы принять их «первородный» вид: А := 1 A = 1 A = 1 В среде Mathcad MM пользователь вышеописанную неопределенность может ликвидировать – замена символов дополнительно ведется по такой схеме:
Эту особенность Mathcad MM автор не стал иллюстрировать отдельным рисунком. Новая схема основных операторов интерфейса «размазана» по рисункам статьи – см. например, рис. 3, где и полуглобальная (S) и локальная (R) переменные объявляются через оператор «:=». 3. «Надсмотрщик» переменныхОдним из самых эффективных инструментов отладки программ[7] считается так называемый Debugger («Надсмотрщик»), позволяющий получить информацию о переменных, задействованных в программе. На рис. 3 показан Mathcad-документ, по которому высчитывается площадь круга. Если «кликнуть» правой кнопкой мыши по блоку операторов, то выпадет локальное меню. В среде Mathcad MM в нем появилась новая команда Debugger. Ее выполнение вызывает на дисплей диалоговое окно Debugger, в котором собрана информация обо всех переменных, задействованных в расчете: имя переменной (Variable), ее тип (Scalar, String, Array – в последнем случае выводится значение (Value) всех элементов вектора или матрицы: V0, V1 и т.д.) и статус (Status). Если переменная размерная, то выводятся соответствующие единицы измерения (Unit).
На рис. 3 все переменные «статичны» – их значение можно изменить, поменяв значение переменной D. Если же в программе задействованы циклы и альтернативы, то переменные становятся «динамичными» – их значения меняются в момент выполнения программы. В этом случае часть информации в окне Debugger начинает изменяться очень быстро. Пользователь может скомандовать «Замри!», нажав следующие кнопки:
4. Размерность валютыMathcad по праву называют не просто математическим, а физико-математическим пакетом. В среде Mathcad переменным можно присваивать не только численные значения (в десятеричном, двоичном, восьмеричном, шестнадцатеричном или римском форматах – см. рис. 23), но и определенную размерность физической величины:
Эта особенность Mathcad существенно упрощает научно-технические расчеты. Ведь часто мы ошибаемся не в формулах (все формулы, лежащие в основе мироздания, просты: F = m·g, E = m·c2 и т.д.) и не в самом расчете (под рукой персональный компьютер или на худой конец калькулятор), а в размерностях (метры – футы, килограммы – фунты, джоули – калории и т.д.). Mathcad не только сопровождает выводимую величину выбранной пользователем размерностью (см. расчет скорости, приведенной выше), но и ведет контроль размерностей, не позволяя, например, складывать длину со временем. Mathcad 2000 (предшественник Mathcad MM) с определенной долей условности можно назвать и финансовым пакетом, так как в него встроено 18 финансовых функций. Вот типичная задача, которую стало возможным решать в среде Mathcad 2000 одним единственным оператором: «Иуда за свое предательство получил 30 серебряников и положил их на депозит под три процента годовых с ежемесячным (ежеквартальным или ежегодным) начислением процентов. Спрашивается, сколько денег у Иуды сегодня окажется в банке[9]?» Доля условности в характеристике Mathcad 2000 как финансового пакета состоит в том, что в Mathcad 2000 не были встроены единицы измерения стоимости так, чтобы финансовые функции возвращали значение, сопровождая их размерностями валюты: доллары, марки, рубли. Можно, конечно, возразить, что стоимость – это не физическая величина. Но физик вполне обоснованно скажет: «У меня на столе лежит книга весом (массой) в один килограмм, толщиной в три сантиметра и стоимостью в 700 рублей». Более того, тот же физик без метров, килограммов, секунд прожить сможет, но без долларов, марок, рублей – никак нет. Тем не менее, наш физик никогда не согласится включить стоимость в стройную систему (там семь основных величин) физических, химических и прочих величин. В Mathcad MM этот недостаток исправлен.
На рис. 4 показано диалоговое окно Insert Units (ввод единиц измерения), где в поле Dimension (Размерность) появилась новая позиция – Currency (Валюта), а в поле Units (Единицы измерения) – название основных мировых валют: американские доллары, немецкие марки, российские рубли и т.д. Механизм размерностей валюты в полном объеме работает лишь в том случае, если компьютер подключен к сети Internet – курсы валют устанавливаются считыванием информации с сайтов центральных банков различных стран. Если Internet недоступен, то текущие курсы валют нужно будет ввести вручную. На рис. 4 решается задача линейного программирования. Суть задачи. Мебельная фабрика может выпускать стулья двух типов: ценою в 70 долларов США и 90 рублей. Под этот заказ выделены доски, обивочная ткань и трудовые ресурсы:
Спрашивается, как нужно спланировать производство стульев, чтобы наваять их ценой поболе. Это и отображено в отчете о решении задачи на рис. 4 – нужно производить 60 стульев первого типа и 80 второго. При этом цена стульев окажется равной 12 840 руб. (10 700 долларов). На рис. 4 читатель может отметить две особенности Mathcad MM. Во-первых, если решается линейная задача, то функция Maximize (Minimize, Find, MinErr) теперь не требует первого приближения. Во-вторых, имена переменных Mathcad MM могут начинаться с цифры: 1-й стул и 2-й стул. 5. Работа с градусами ЦельсияДля работы с единицами измерения физических величин, отсутствующими в списке встроенных в Mathcad, необходимо пользовательские единицы привязать к встроенным через соответствующие множители. Пример: пуд := 16 kg Но это правило нельзя применить к температуре. Дело в том, что по отношению к этой физической величине существуют два понятия – единица измерения температуры (градус Кельвина, градус Цельсия, градус Фаренгейта и др.) и шкала измерения температуры (шкала Кельвина, шкала Цельсия, шкала Фаренгейта и др.). Шкала Цельсия – внесистемная шкала, которая тем не менее широко используется для отображения значения температуры. В расчетах же, как правило, оперируют температурой, выраженной по шкале Кельвина (Европа) или по шкале Ренкина (США). Формулы перевода температуры из одной шкалы в другую довольно просты, но в них не вписывается принятая технология ввода пользовательских, включая и внесистемные, единиц измерения. В среде Mathcad MM эта проблема решена – см. рис. 5.
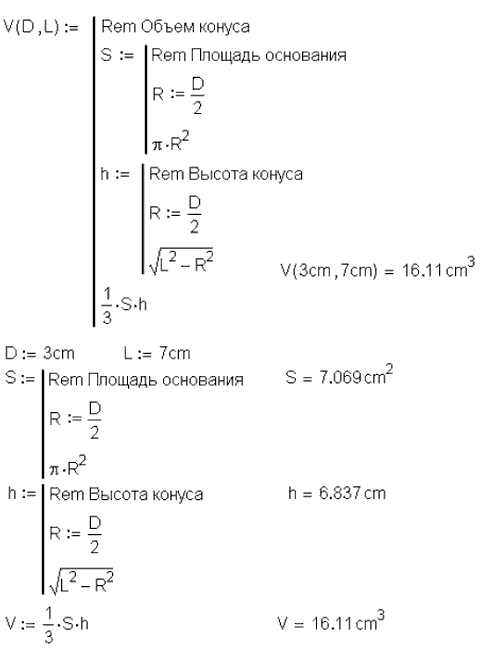
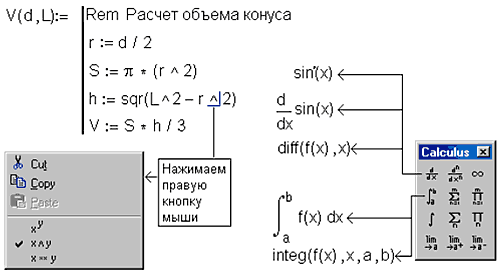
Теперь в списке встроенных единиц измерения температуры есть не только градусы Кельвина и Ренкина, но и градусы Цельсия (Celsium в европейской версии и Centigrade – в американской), Фаренгейта и Реомюра: «Стоял прекрасный июльский день. А прекрасен он был потому, что было 25 градусов по Реомюру» (Вс. Гаршин) – см. последнюю строку на рис. 5. 6. Суперлокальная переменнаяВ пункте 2 нашей статьи, описывая альтернативные символы операторов ввода значений переменных и функций («º», «:=» и «¬»), мы подчеркнули иерархию переменных: глобальная, полуглобальная (полулокальная) и локальная. В среде Mathcad MM эта градация стала еще более сложной: локальность переменной теперь ограничивается не только программой, но и отдельным программным блоком. Вот Mathcad-программа, по которой вычисляется объем конуса[10] (рис. 6):
Спрашивается, зачем нужно было при формировании функции V(D, L) дважды вычислять радиус основания конуса R – при расчете площади основания конуса S и при расчете его высоты h? Дело в том, что в среде Mathcad MM переменная видна только в том блоке операторов, где она была объявлена оператором присваивания. Данный блок очерчен вертикальной чертой. Переменная, объявленная в этом блоке (у нас это переменная R), видима в блоках, вложенных в данный блок («видимость» сверху вниз), но невидима в соседних блоках, как это было в старых версиях Mathcad. Вертикальные линии, отмечающие начала и концы программных блоков, в среде Mathcad MM стали полупрозрачными. Это сделано для того, чтобы не возникали проблемы при отладке программ разъятия ее на отдельные блоки – см. нижнюю часть рис. 6. В среде Mathcad MM стало удобным не только отлаживать программы их разъятием (сравните верхнюю и нижнюю части рис. 6), но и создавать программы сбором отдельных отлаженных операторов (нижняя часть рис. 6) в единый программный блок (верхняя часть рис. 6). Другой резон – пользователь теперь может спокойно переносить программные блоки в новый Mathcad-документ, не боясь «потерять» часть переменных. 7. Мастер функцийMathcad MM имеет более совершенный инструмент, который принято называть «Мастер функций». Вот перечень новых возможностей вставки в Mathcad-документ встроенных функций через диалоговое окно Insert Function (Вставить функцию – см. рис. 7).
Более «интеллектуально» в среде Mathcad MM стал осуществляться ввод встроенных функций Find и MinErr. Если пользователь забыл предварить ввод этих функций записью в Mathcad-документе ключевого слова Given, то Мастер функции это сделает сам. Пользователю остается только «перетащить» это слово в нужное место так, чтобы Given и Find (MinErr) охватывали группу уравнений и/или неравенств. 8. Древовидный оператор с более чем двумя ветвями операндовВ старых версиях Mathcad древовидная форма вызова была допустима
только к функциям с двумя аргументами. В среде Mathcad MM древовидно можно
вызывать функцию с любым числом аргументов. Получаемое при этом «дерево»
будет иметь не два, а более ветвей, если в среде Mathcad MM нажать кнопку
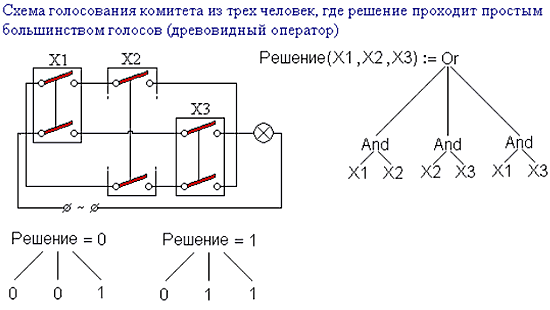
На рис. 8 в качестве иллюстрации показано формирование функции Решение, возвращающей вердикт жюри присяжных, состоящего из трех голосующих. Встроенный оператор And имеет две ветви, а встроенный оператор Or – три. На рис. 8 показано и аппаратное решение этой задачи – схема шести выключателей, соединенных последовательно (And) и параллельно (Or). 9. Древовидные встроенные операторыВ среде Mathcad функцию с двумя аргументами «тридиционно» можно вызывать тремя способами:
В старых версиях Mathcad инфиксную и древовидную форму вызова функций, к сожалению, нельзя было применить к встроенным операторам. В среде Mathcad MM этот недостаток исправлен. Теперь встроенные операторы сложения, вычитания, деления и умножения можно вызывать в виде не только инфиксных, но и древовидных операторов. 10. Две переменные ORIGINВ среде Mathcad MM системная переменная ORIGIN «распалась» на две новые переменные – ORIGINR и ORIGINC, хранящие номер верхнего ряда матрицы (номер первого элемента вектора-столбца) и номер левого столбца матрицы соответственно[11]. По умолчанию эти переменные хранят нули. Рекомендуется не трогать эти переменные, а «сдвигать» индексацию элементов массивов другими способами. Но те пользователи Mathcad, кто привык реализовывать свои алгоритмы через изменение индексации «начала» массива, оценят преимущества двойной переменной ORIGIN. 11. Given в программеВ среде Mathcad MM встроенные функции Find и MinErr обязаны работать с ключевым словом Given, а функции Minimize и Maximize – могут. Перед функциями Find и MinErr должна быть записана система алгебраических уравнений и/или неравенств, перед функциями Minimize и Maximize может быть записана система ограничений процесса оптимизации. В среде Mathcad MM наконец-то стало возможным вставлять ключевое слово Given в программы. Теперь можно решать алгебраическое уравнение в программном блоке, вставляя в него функции Find и MinErr. Кроме того, в программах допустима оптимизация с ограничениями за счет предварения функций Minimize и Maximize ключевым словом Given.
На рис. 11 показано формирование (переопределение) функции Find, возвращающей корни системы алгебраических уравнений, графическое решение которых показано на рис. 1. Обновленная функция Find имеет такой же синтаксис, как и у функций Minimize и Maximize. 12. Структурирование Mathcad-документаНа рис. 12 показано три вида Mathcad-документа расчета объема конуса. Верхняя часть рис. 12 – это название документа (комментарий) и горизонтальная черта, отмечающая захлопнутую область, куда поместили все расчеты. Если эту область раскрыть, то пользователь увидит среднюю часть рис. 12: заголовок и распахнутую область, внутри которой три подзаголовка и три новые захлопнутые области, содержимое которых, в свою очередь, показано (распахнуто) в нижней части рис. 12.
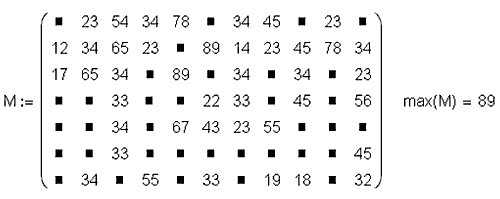
Возможность выделения в Mathcad-документе области (областей одного уровня) для последующей ее защиты от редактирования (Lock) появилась в седьмой версии пакета. В восьмой версии эти области стало возможно захлопывать (Collapse). В среде Mathcad MM снят запрет на создание вложенных областей внутри ранее созданных, чем мы и воспользовались, формируя рис. 12. 13. Разреженная матрицаСтарые версии Mathcad требуют, чтобы в матрице (в векторе) абсолютно все элементы были определены пользователем или системой. Но при решении задач нередко возникает ситуация, когда некоторые элементы массивов должны оставаться пустыми. Пример – необходимо определить максимальный возраст человека, сидящего в кинотеатре, где зрители прикреплены к рядам (строки матрицы) и местам (столбцы матрицы) кресел в зале, который далеко не всегда имеет «прямоугольную» форму, подразумевающую одинаковое количество мест во всех рядах. Кроме того, не все места в зале бывают заняты. Для Mathcad MM это не проблема – см. рис. 13:
В связи с этим (возможность работы с разреженными матрицами) были пересмотрены все встроенные «матричные» функции и операторы Mathcad. Часть из них может работать с «полупустыми» матрицами и векторами (это функции max, min, mean и др.), а другие (например, оператор вычисления детерминанта квадратной матрицы) – нет. В среде Mathcad MM стало удобнее интерполировать сплайном данные двухфакторного эксперимента. Теперь исходная дискретная информация может быть не только «квадратной», но и «прямоугольной» с отсутствующими точками (см. рис. 13). Описанная особенность, как понимает читатель, перешла в Mathcad из Excel, где функции умеют игнорировать ячейки электронной таблицы, содержащие нечисловую или «пустую» информацию. В среде Mathcad MM «умеют» оставаться пустыми не только элементы массивов (см. рис. 13), но и переменные: А := 3 В := 3 if A › 0 В вышеприведенном фрагменте Mathcad-документа переменная В остается пустой (необъявленной) или сохраняет свое прежнее значение, если в переменную А введено неположительное число. В старых версиях Mathcad второе выражение (там записана альтернатива с одним плечом) всегда давало сбой. В среде Mathcad MM введены изменения и в работу встроенной функции if. Теперь она может иметь не только три, но и два или четыре аргумента:
14. Многомерная матрицаОдно из отличий массивов в среде Mathcad от массивов традиционных языков программирования состоит в том, что массив Mathcad – это либо вектор (одномерный массив), либо матрица (двухмерный массив). В среде BASIC можно объявить и «более двухмерный» массив: Dim M (0 to 1, 0 to 1, 0 to 1) As… В среде Mathcad MM стало возможным работать не только с «линейными» и «плоскими» (вектор и матрица), но и с «объемными» массивами – см. рис. 14[12].
Оператор М‹n› фиксирует n-й столбец плоской матрицы, а оператор ‹n›ММ – n-й слой. Ввод в среду Mathcad MM многомерных массивов потребовал пересмотра всех «матричных» функций и операторов, не все из которых способны работать с «объемными» массивами. 15. Расширенный оператор выводаВ среде Mathcad MM допустимо строить цепочку вывода значений переменной функции – рис. 15.
Цепочка операторов вывода получается просто: достаточно несколько раз нажать на клавишу «=». После этого будут выведены на дисплей рассчитанные значения с форматом умолчания, который пользователь вправе изменить, дважды «кликнув» выведенное число. При этом допустимо задействовать все опции диалогового окна Format Number: менять форму записи числа (General, Decimal, Scientific, Engineering), число выведенных цифр, наличие мантиссы и т.д. Это можно было делать и в старых версиях Mathcad, дублируя оператор вывода: f(x) =… f(x) =… и т.д. Но Mathcad MM обладает еще одной возможностью – он позволяет выводить не только число (View as value – умолчание), но и формулу, по которой выводимое значение рассчитывается (см. команду View as formula…[13] в меню на рис. 15). 16. Группировка данных в записьВ старых версиях Mathcad векторы и матрицы хранят либо безразмерные величины (числовые константы или тексты), либо величины с одинаковой размерностью (длина, время, давление и т.д.). Объединение разнотипных («разноразмерных») величин в одном массиве прерывалось сообщением об ошибке, так как массивы – это объединение сугубо однотипных величин («бутылки в ящике»). Разнотипные величины («разноразмерные» – «бутылки в баре») можно собрать в записи, что стало возможным в среде Mathcad MM – см. рис. 16, где формируется функция пользователя, возвращающая параметры конуса – радиус и площадь основания, его высоту и объем. Аргументы функции – диаметр основания конуса и длина образующей. Если аргументы функции — безразмерные величины, то наша функция безаварийно работает во всех версиях Mathcad. Если же аргументы – размерные величины (длина), то функция безаварийно работает только в среде Mathcad MM. Это очень удобно при отладке программ[14], когда необходимо массивом (записью) вывести значения всех локальных переменных с их размерностями.
Ввод в среду Mathcad MM записи (record) потребовал пересмотра всех встроенных функций и операторов, работающих с массивами. Так, например, функции min, max, mean, gmean и др. работают только с массивами (с записями, элементы которых – однотипные переменные). Вычисление детерминанта квадратной матрицы требует, чтобы строки матрицы хранили однотипные переменные. Такое же условие предъявляет встроенная функция rsort («строковая» сортировка матрицы – сортировка перестановкой столбцов). Функция же csort (сортировка перестановкой строк), наоборот, требует одноразмерности по вертикали и т.д. 17. Решение задачи линейного целочисленного и дискретного программированияВ пункте 4 нашей статьи для иллюстрации новой размерности (стоимость) мы решали задачу линейного программирования – нашли оптимальный план выпуска стульев, при котором их стоимость максимальна, а лимит по ресурсам не превышен. Но на рис. 4 целые значения плана выпуска стульев (1-й стул:= 60 шт., 2-й стул:= 80 шт) получились случайно. Честно говоря, автор специально подобрал значения коэффициентов этой линейной задачи так, чтобы получился целочисленный ответ. Но Mathcad MM может решать задачи целочисленного и дискретного линейного и нелинейного программирования (рис. 17).
В среде Mathcad ММ можно «кликнуть» правой кнопкой мыши по одному из аргументов функции Maximize[15] и вызвать тем самым диалоговое окно Options of Var, нацеливающее на поиск целочисленного решения (integer или integer ≥ 0). Позиция discret… вызывает дополнительное диалоговое окно, где пользователь может записать дискретные значения, которые будут присваиваться переменной при решении оптимизационной задачи. 18. Альтернативные математические операторыВ среде Mathcad 2000 появилась возможность изменять символы операторов умножения и деления. Деление, к примеру, можно записывать не только столбиком (числитель вверху, знаменатель внизу), но и строкой: a¸ b. В среде Mathcad ММ умножение имеет еще больше альтернативных символов-дублеров: a × b, axb, a b, ab и др. В среде Mathcad MM почти все математические операторы продублированы. Вот некоторые примеры:
Альтернативное написание операторов позволяет, во-первых, приблизить программы Mathcad к их аналогам, написанным на языках Pascal, C, Basic, Fortran – – см. правую половинку рис. 18.
Теперь стало возможным переносить в среду Mathcad целые фрагменты, написанные на этих языках. Кроме того, паскалезированные (бейсиколизированные) Mathcad-программы более компактны – см. рис. 18. 19. Нечеткая логикаВ среду Mathcad MM встроен один булев оператор с одним операндом (логическое отрицание) и пять булев операторов с двумя операндами: «=» – равно; «¹» – не равно; «Ù» – логическое умножение (и); «Ú» – логическое сложение (или); «Å» – исключающее «или». Последние три оператора появились только в Mathcad 2000. В среде Mathcad MM внесены изменения в работе данных двухместных булевых операторов. Во-первых, если говорить о вычислительной математике (о численных методах решения задач ), то здесь оператор «равно» почти не используется. Тут нужен другой оператор – «примерно равно». Если в среде Mathcad MM пользователь «кликнет» правой кнопкой мышки символ «=», то появится локальное меню, позволяющее оператор «a = b» заменить, во-первых, на оператор «= =» (см. пункт 2) или на оператор «примерно равно» – «a » b», эквивалентный такой Mathcad-конструкции ½ a - b½ £ TOL. Такая же метаморфоза допустима и в отношении оператора «не равно» (½ a - b½ > TOL). На рис. 19 показано формирование функции пользователя, возвращающей корень алгебраического уравнения.
В программу на рис. 19 заложен метод половинного деления – приближение к корню ведется, пока переменная a «примерно не равна» (далеко отстает от) переменной b: Второе новшество. В среде Mathcad MM операторы Ù , Ú и Å (функции And, Or и xOr) правильно работают не только с булевыми операндами (нет – ноль, да – число, отличное от нуля), но и с вещественными операндами, плавно меняющимися от 0 до единицы (до 100 процентов). Это позволяет реализовывать в среде Mathcad MM элементы теории нечеткой логики:
Третья особенность блока булевых операторов Mathcad MM заключается в том, что в него добавлены операторы «намного больше» и «намного меньше». a >> b эквивалентно a > b· TOL a << b эквивалентно TOL·a < TOL 20. Многоязычные комментарииВ пункте 22 будет описан новый оператор Mathcad MM, позволяющий вводить в Mathcad-программы комментарии. Rem Комментарий Данный оператор допустимо использовать и вне программ для вставки тех же ремарок.
Более того, «кликанье» по данному оператору правой кнопкой мыши вызывает локальное меню с такими дополнительными возможностями (рис. 20):
21. Псевдоним переменной, функции и оператораПсевдоним (или кличка) – это, можно сказать, локальное имя переменной во времени и пространстве. В среде Mathcad MM переменным, функциям и операторам можно давать дополнительные имена. В католических странах считается, что если человеку при рождении дали много имен (одно из них считается главным), то этот человек проживет счастливую жизнь, так как его будут опекать много святых-тезок. Как в среде Mathcad MM переменным функциям и операторам даются дополнительные имена? Во-первых, у имен функций и операторов есть дополнительные встроенные имена и символы – см. рис. 20. Во-вторых, переменной можно дать дополнительное пользовательское имя. Это делается просто. Переменная (имя функции или символ оператора) «окликаются» правой кнопкой мыши, что вызывает на экран контекстное меню. В среде Mathcad MM в этом меню среди привычных команд (Copy, Property и т.д.) есть и новая – New Name... Три точки за именем команды означают, что ее выполнение будет предваряться дополнительным диалогом, где пользователь выскажет свои пожелания по новому (дополнительному) имени переменной функции или оператора. Для чего переменным и другим объектам Mathcad даются новые имена? Во-первых, дополнительное имя объекта используется как комментарий, подсказка пользователю. Если к имени объекта подвести курсор мыши, то выпадет табличка с дополнительными именами. Во-вторых (это касается встроенных переменных и функций), пользователь имеет возможность в Mathcad-документе менять имя переменной (функции, команды) на национальное или на более развернутое: Пример:
М:= augment(2)
М:= Единичная матрица размером 3 «Псевдоним» функции в приведенном примере дополнительно выполняет роль комментария. 22. ПрограммированиеМы уже коснулись некоторых новшеств Mathcad ММ, связанных с программированием:
На рис. 22.1 показана панель программирования Mathcad ММ с пятью новыми кнопками:
В программе Mathcad MM наконец-то стало возможным записывать комментарии. Для этого нажимается кнопка Rem, а затем в появившейся заготовке Rem ■ placeholder (■) заполняется комментарием – цепочкой символов (см. рис. № ...). Кнопка Cycle вводит в программу бесконечный цикл, который можно прервать «старыми» операторами Mathcad – break, continue и return. В нижней части рис. 22.1 создается функция пользователя, возвращающая корень алгебраического уравнения. В программу заложен цикл с выходом из середины – более универсальная алгоритмическая конструкция, чем привычный цикл while. Кнопки Label и Goto позволяют реализовывать в Mathcad-программах разветвленные алгоритмы через метки и операторы условного безусловного перехода к меткам. Кроме того, инструменты Label и Goto можно вставлять вне программ в Mathcad-документы для реализации метода последовательных приближений без программирования. Кнопка Add Operator позволяет в Mathcad-программе записывать несколько операторов в одной стороне, что делает программы более компактными. Претерпел изменения в среде Mathcad ММ и оператор if. Теперь после нажатия на одноименную кнопку панели программирования появляется такая заготовка: if ■ then ■ else ■ Если пользователь сотрет в данной заготовке два правых placeholder’а, то он получит привычную в среде Mathcad заготовку оператора «альтернатива с одним плечом»: ■ if ■ На рис. 22.2 показана программа поиска корня уравнения с новой альтернативой.
В среде Mathcad ММ пользователь может объявлять в программном блоке не только локальные переменные, но и локальные функции. На рис. 22.3 показана программа с локальной функцией.
23. Римская математикаВ старой версии Mathcad вычисления были возможны в одной из четырех систем:
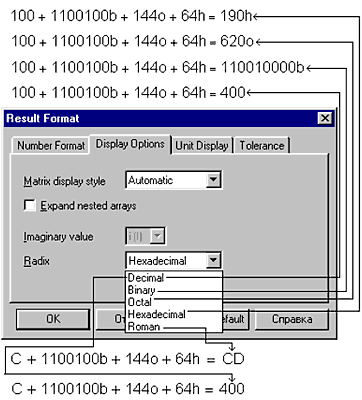
На рис. 23 показано, как складываются четыре сотни, введенные пользователем в десятеричном (100), двоичном (1100100b), восьмеричном (144о) и шестнадцатеричном (64h) форматах. Ответ при этом также выводится в различных форматах. Mathcad-оператор «=» по умолчанию выводит численные значения в десятеричном формате. Изменение формата ведется через диалоговое окно «Result Format (рис. 23), вызываемое на дисплей двойным щелчком по результату (или через общее или контекстное меню).
В среде Mathcad MM расчеты можно вести, используя и римские числа. Для ввода таких чисел используются цепочки символов М, D, C, L, X, V и I. Перевод числового результата в римскую нотацию ведется через диалоговое окно Result Format, где появилась новая позиция Roman – см. рис. 23. Римские числа используются не только для нумерации часов на некоторых циферблатах и не только счета глав в книгах. С римскими числами мы имеем дело... ведя денежные расчеты. Дело в том, что сумма денег – это арабское число, а ее разложение на банкноты и монеты – римское число. Сравните: 271 = CCVXXI 271 р = 100 р + 100 р + 50 р + 10 р + 10 р + 1 р Алгоритмы перевода чисел из арабской в римскую нотацию, и наоборот, встроенные в Mathcad MM, пригодятся, например, в работе банкомата. 24. Системные переменные по параметрам атмосферы и пользователяПо особому заказу пользователя вместе с пакетом может поставляться особое устройство, похожее на электронный ключ[18], вставляемое в компьютер на входе кабеля принтера (или, например, в разъем USB). Это устройство называется SmartPhysic и выполняет следующие функции:
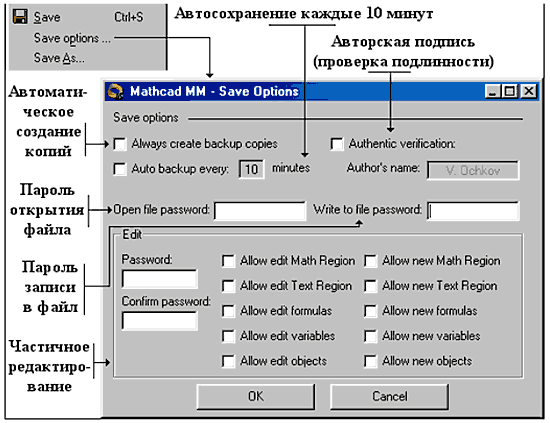
25. Сохранение документаВ Mathcad MM значительно расширены возможности по сохранению файлов. Теперь можно задать пароли для открытия файла, записи в файл и специальный пароль для редактирования. На рис. 24 показано диалоговое окно настроек сохранения файлов, которое вызывается в меню File выбором пункта Save options…..
Как видно из рис. 24, в Mathcad MM появилась возможность создания копий рабочего файла, а также автоматическое сохранение через заданный промежуток времени. Как уже упоминалось выше, с помощью устройства SmartPhysic становится доступной цифровая подпись документов Mathcad. Это позволяет точно удостоверить автора документа, так как без наличия SmartPhysic внесенные в файл изменения разрушают авторскую информацию. В поле Author’s name Mathcad MM заносит значение переменной UserName, считанное с устройства SmartPhysic. Пароли для открытия и сохранения файла позволяют ограничить доступ к файлу. Принцип их действия такой же, как и в продуктах семейства Microsoft Office, поэтому на них останавливаться не будем, а перейдем сразу к следующему нововведению. Разработчики Mathcad MM пошли дальше по пути ограничения доступа к документам, чем их соперники из группы разработки Microsoft Excel[20]. В новой версии Mathcad автор документа (и не только) может указать, какие изменения допустимы, а какие требуют знания пароля. Это позволяет защитить такие составляющие документа Mathcad, как данные, формулы, текст или внедренные объекты, каждый в отдельности или в сочетаниях. Все это настраивается во фрейме Edit путем выбора необходимых настроек. 26. Сумма в числовом ответеВ среде Mathcad оператор «=» выводит на дисплей числовое значение переменной, функции, выражения: p = 3.14, sin(0) = 0, 5 + 3 = 8 и т.д. При этом пользователь имеет возможность разбить ответ на два сомножителя, припечатав к ответу какую-либо числовую константу или переменную, хранящую число:p=1•p, 5 + 3 = 2•4 и т.д. Как правило, этот прием используется для изменения единиц измерения выводимой размерной величины: 2 m+30 cm=2.3 m, 2 m+30 cm=230 cm (2300 mm), s := 10 acrе s = 405 m 10 m и т.д. В среде Mathcad MM числовой ответ можно не только представить в виде произведения (факторизация), но и в виде суммы. Примеры: 130 min = 2.5 hr 130 min = 2 hr + 30 min 165.1 cm = 5 ft + 5 in 195.58 cm = 2 аршина + 12 вершков 30.51° = 30° + 30¢ + 36² и т.д. Кроме того, в подобных примерах символ сложения «+» можно заменять на побел: 252.365cm=3 аршина 2 пяди 1 вершок Разложение ответа на слагаемые очень удобно для отображения величин, единицы измерения которых не кратны 10: время, углы, суммы старинных денег (гинеи, шиллинги, гроши, полкопейки и т.д. ).Ответ же разлагается на сомножители просто. Для этого достаточно охватить ответ курсором, нажать на клавишу плюс (один или несколько раз) и ввести в ответ встроенные (hr, min и др.) или пользовательские (аршины, вершки и др.) переменные, хранящие единицы измерения. 123. Лишение переменной и функции ее числового
значения (Deprivation variable (function) of its
numerical value (definition))
124. Связь
между переменными (Variables Links) (Mathcad)
125. Более точное комментирование символьных преобразований126. Оператор вывода работает и по отдельным
переменным (The operator of a evaluate numerically works
and on separate variable in Expressions)
127.
Функция RND работает и с массивом (RND-function works with array too)
128. Функция RND работает и с переменной области (RND-function works with Range
Variable too)
ЭпилогВ старые времена в «Литературной газете» была очень популярна рубрика «Если бы директором был я...». Это было своего рода «будка гласности», где все желающие могли высказаться о наболевшем, о том, как можно подправить наши дела. Интересно, на какой позиции читатель этой статьи понял, что его разыгрывают. Да, дорогой читатель, – это первоапрельская шутка – статья помещена в апрельском номере журнала. Вернее, планировалась к публикации в апреле 2000 года... Но до апреля еще далеко. Может выйти новая (подправленная) версия Mathcad с реализацией некоторых вышеизложенных идей. Статья по Mathcad 2000 планировалась к публикации в11-м номере журнала КомпьютерПресс, но по ряду причин вышла только в 12-м номере за 1999 г. Аналогичная история может случиться и со статьей по Mathcad MM – она может выйти не в апреле, а, к примеру, в мае. Поэтому нет ничего страшного в том, что «первоапрельская» статья попала в декабрьский номер журнала. В любой выдумке должна быть доля истины. Данной статье место в журнальной рубрике «Если бы разработчиком программы был я...». Жанр статьи можно отнести к разряду научно-фантастического программирования. Конечно, никакого пакета Mathcad MM в природе нет[21], а есть желание улучшить Mathcad. Автор надеется, что его электронный адрес ochkov@twt.mpei.ac.ru станет своеобразным «дуплом», куда пользователи Mathcad могут складывать свои соображения. P.S. Можно считать, что авторы провели с программой Mathcad «сеанс магии». Но многие «фантастические» пункты статьи, кстати, близки к реальности. Описанные инструменты работы с Mathcad-документами с некоторыми хитростями работают и в среде реального пакета. Читатели вправе требовать «разоблачения». Они (разоблачения – реализации описанных идей и фантазий) будут помещены в книге авторов «Mathcad и MathConnex для профессионалов», готовящейся к выпуску в издательстве «КомпьютерПресс». [1]К числу 2000 в компьютерном мире
существует некое предубеждение. Как к числу 666 в религиозном мире. Число
2000 у многих людей ассоциируется не с новым веком (он,
кстати, начнется не в 2000 году, а в 2001-м – нулевого года в нашей эре не
было) и не с новыми возможностями новых программ, а с... ошибкой двухтысячного
года (некий локальный компьютерный апокалипсис). [2]Действительные корни системы мы найдем
численно в пункте 11 нашей статьи. [3]Отсюда можно сделать вполне закономерный
вывод о том, что первые версии Mathcad писались на языке Pascal. [4]Это является прямым следствием политики фирмы Microsoft, которая перестала поддерживать линию языка Pascal, полностью переключившись на Visual C и Visual Basic как на основные инструменты создания Windows-приложений. Операционную систему Windows, так же, кстати, как и Mathcad, сначала писали на языке Pascal. Но потом разработки перешли на С. [5]Этим пользователь
страхует себя от случайного переопределения встроенной или пользовательской
переменной. [6]В среде Mathcad ММ, кстати, placeholder
может оставаться пустым – см. пункт 13 нашей статьи. [7]В среде Mathcad 2000
появился наконец-то первый инструмент отладки – трассировщик ошибок. [8]Точка останова – это
рутинный инструмент отладки программ, написанных в средах традиционных языков
программирования. Но в среде Mathcad MM можно пометить отдельный оператор на
строке, содержащей много операторов. [9]Ответ одного из студентов, обучающихся у
автора: «Если это был российский банк, то ни копейки. 17 августа 1998 года
Иуда потерял все свои деньги и еще раз повесился. Если же
ему удалось сохранить вклад или хотя бы часть вклада, то неизвестно, что с
ним (и с вкладом, и с банком) станется после 1 января 2000 года». [10]Этот нехитрый расчет мы еще не раз повторим,
иллюстрируя те или иные новинки Mathcad ММ: см. пункты 12, 16 и 18. [11]В среде Mathcad ММ переменных ORIGIN
может быть более двух – см. пункт 14. [12]Приставку ММ можно рассматривать не
только как «2000» или «More Mathematic» (см. пролог), но и как «Многомерный
Массив». [13]За именем команды следует многоточие,
означающее, что последует уточняющий вопрос о том, записывать ли в формулы
переменные или константы. [14]В среде Mathcad MM снято ограничение на
использование размерностей физических величин в
программах. [15]Можно, «кликнув» и по первому аргументу
функции Maximize, наложить ограничение по целочисленности
и на целевую функцию. [16]Этот оператор совпал по написанию с
оператором логического умножения. [17]Это и понятно – из Maple V в Mathcad
взята символьная математика. [18]Такой ключ поставляется с русской
версией Mathcad 6 для защиты пакета от незаконного копирования. [19]Рекомендуется приобретать специальный
удлиненный кабель для принтера, в середину которого (кабеля) вклинивается
устройство SmartPhysic. [20]Как известно, «предком» Mathcad была
электронная таблица, то есть аналог Excel. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||