Формулы[1] научно-технических публикациях: проблемы и решения
Автор с коллегами готовил к изданию справочник по теплофизическим свойствам теплоносителей и рабочих тел энергетики [1], который поддерживается сайтом http://twt.mpei.ac.ru/rbtpp с сетевыми, интерактивными, открытыми расчетами [2-7]. Справочник содержит, в частности, описание сайта. При подготовке этой части рукописи и отладке сайта возникла необходимость соединить в одном тексте общепринятые математические нотации и специальные формы записи математических выражений в компьютерных математических программах. Здесь автор хочет рассказать о возникших проблемах и возможных способах их решения.
Обращаем внимание на важность данной проблемы - см. >>>
В настоящее время в научно-технических публикациях (монографиях, учебниках, справочниках, диссертациях, авторефератах, журнальных статьях, студенческих курсовых и дипломных работах и тд) все чаще и чаще формулы представляют собой не наборы символов, введенных «от руки»[2] или с помощью специальных программ Word Equation (дополнение к Word), LaTex и др., а фрагменты расчетов, сделанных в средах компьютерных математических программ Mathcad, Maple, Mathematica и др. (см. сайт www.exponenta.ru, их поддерживающий). Более того, отмеченные математические программы имеют собственные средства комментирования расчетов, что позволяет с их помощью полностью готовить рукописи[3] к публикации, не прибегая к специализированным программам – текстовым процессорам Word, Adobe Acrobat и др.
Наиболее распространенной является компромиссная технология, когда автор передает в издательство или редакцию журнала «гладкий» текст в файле формата doc и растровые рисунки в отдельных файлах формата bmp, например. Затем специалисты издательства объединяют эти файлы и готовят публикацию по стандартам издательства.
В bmp-файлах могут храниться не только традиционные рисунки (схемы, фотографии, диаграммы, графики), но и формулы в виде скриншотов (screen shot – моментальный фотоснимок, слепок с экрана компьютера[4]) протоколов решения задач в средах математических программ.
Отказ от прямого набора формул в тексте и обращение к услугам «посредников» – математических программ объясняется рядом причин, одна из которых в том, что ручной набор формул без проверки их работоспособности (а она-то и ведется в математических программах) часто чреват ошибками, которые допускает автор и пропускают редакторы и корректоры при работе над рукописью или макетом книги или журнальной статьи. Вспомним, сколько ошибок и опечаток мы допускали в текстах, когда писали их на бумаге или набирали на печатной машинке или компьютере без вшитых средств проверки орфографии (спел-чекеры)! Можно сказать, что в математические пакеты вшиты средства проверки «орфографии формул», высвечивающие в них возможные ошибки. Но главная причина обращения к математическим программам в том, что в настоящее время именно в средах математических программ, как правило, ведется обработка результатов экспериментальных данных, формирование таблиц, построение графиков или оценка теоретических вкладок с показом итоговых и промежуточных результатов. Плоды такой работы желательно перенести в готовящуюся публикацию без каких-либо искажений. Есть и другие причины «экспансии» математических программ в публикации, которые будут раскрыты ниже.
И тут возникает ряд проблем, требующих решения.
1. Проблема десятичного разделителя (decimal separator)
Россия принадлежит к странам, где традиционно в качестве десятичного разделителя используется запятая. В других странах (а это, в основном, англоязычные страны) используется точка. Главная англоязычная страна США в настоящее время задает тон в информационных технологиях. Поэтому все основные компьютерные программы, даже если они сделаны в России, оперируют точкой в качестве десятичного разделителя[5]. Из-за этого в книгах, научных статьях и других публикациях формулы, перенесенные в текст из математических пакетов, содержат точки, в то время как числа самого текста, поясняющего формулы, – запятые. Попытки авторов ликвидировать этот разнобой – поставить в числах текста точки, а не запятые жестко пресекаются редакторами[6] и корректорами, которые стоят на страже издательских стандартов, в частности, правила, устанавливающего, что в «отечественных» числах целую и дробную части может разделять только запятая, но никак не точка. Более того, некоторые редакторы и почти все корректоры требуют, чтобы и в «компьютерных» формулах точки в числах были заменены на запятые. И только возражения авторов в том плане, что это не просто формулы, а слепки с экрана дисплея, где данная задача решалась с помощью конкретной математической программы, что в этом рисунке ничего нельзя менять, иначе это будет некий обман читателей, что если точки в числах заменить на запятые, то нужно запятые, которые используются как разделители в списках, менять на точки с запятой, а точки с запятой (а это тоже узаконенный символ в программах) еще на что-то другое[7] и т.д., переубеждает редакторов и корректоров, но далеко не всегда. Если же автор сдастся и заменит в числах формул точки на запятые, то это будет не просто обман (см. выше), но и некая «медвежья услуга» читателю со стороны автора вкупе с редакторами и корректорами. Читатель захочет ввести формулу с листа книги или журнала в компьютер, проверить ее или решить с ее помощью свою задачу[8] и не будет понимать, почему у него это не получается…
Тут можно узреть некую войну точки с запятой, которая… Тут автор хотел сказать «не стоит выеденного яйца», но вспомнил более литературную «яичную» аналогию. Джонатан Свифт в своих книгах о похождениях Гулливера[9] описал войну тех, кто разбивал яйцо с тупого конца (запятая) с теми, кто это делал с острого конца (точка)…
В настоящее время многие страны с высоким уровнем информатизации, где традиционно использовалась и используется запятая в числах (Германия, например[10]), постепенно переходят на точку. Недавно один немецкий коллега подарил автору данной статьи свою новую книгу и особо просил сообщить, если в тексте вместо точки в числе окажется «устаревшая» запятая. В этом деле и нам наконец-то нужно «поставить точку» в прямом и переносном смыслах… Этот процесс уже пошел – некоторые наши издательства полностью перешли на точку в числах. Правда, эти издательства выпускают специфическую литературу – переводы (часто машинные) с английского на русский технических текстов, не подвергнутые более-менее тщательной научной редактуре[11]. Тут можно отметить и некую «фронду[12]», нацеленную против закостенелых правил, изолирующую страну от «полиграфического мейнстрима». Так в России в начале XX века некоторые передовые литераторы писали и публиковали свои тексты, отказываясь от старой русской орфографии с ятями, тремя буквами «и»[13] (кошмар гимназистов старых времен), лишними твердыми знаками на конце многих слов и тд. Потом, правда, уже после революции 1917 года некоторые из этих «передовиков» уже в эмиграции издавали свои газеты и журналы, используя старую орфографию в пику «совдеповским» изданиям. Более свежий пример. Во времена еще одной нашей «революции» – перестройки 80-90-х годов прошлого века радикальные «западники» вели разговоры о том, что России нужно срочно переходить с кириллицы на латиницу[14]. Некоторые газеты и журналы в те времена демонстративно публиковали статьи и заметки латиницей, а не кириллицей[15]. При этом подчеркивалось, что латиница поможет нам быстрее приобщиться к западным ценностям (истинным и, как мы потом узнали, к ложным) , а процесс компьютеризации у нас пойдет более быстрыми темпами и т.д. Были попытки перевести на латиницу татарский язык. Но потом все эти проекты и эксперименты были пресечены охранительным законом, гласящим, что письменность всех народов Российской Федерации может использоваться только на кириллице. Отсылаю читателя к роману Дмитрия Быкова «Орфография», где эта тема развита, естественно, более глубоко.
Можно представить себе, что если жизнь все-таки заставит нас перейти от запятой к точке в числах, то найдутся люди и издания, которые демонстративно будут тут ставить запятую, подобно тем парижским мальчишкам, которые когда-то давно демонстративно продолжали играть во фронду (игру с пращей) после того, как ее из-за многочисленных несчастных случаев запретила полиция[16].
Проблема точки или запятой в числах усложняется еще и тем, что существует так называемый международный финансовый формат чисел (###,###,###,###.##), где запятая выступает в качестве тысячного разделителя, а точка отделяет рубли/доллары от копеек/центов. Но в инженерно-технических и научных расчетах такая избыточная точность, как правило, не требуется и числа округляются (к проблемы округления чисел мы еще вернемся ниже, когда будем говорить о «живых» задачниках) даже в так называемых технико-экономических расчетах, где наряду с физическими величинами (массой, энергией, временем и тд – см. раздел 6) используются и финансовые.
2. Проблема имен переменных в формулах
Проблема «кириллицы – латиницы» в формулах, затронутая выше, высвечивается с еще одной интересной стороной.
Переменные в «отечественных» формулах могут содержать как буквы кириллицы, так и латиницы, а также буквы греческого алфавита[17] и различные спецсимволы. В научных дисциплинах есть величины (константы и переменные), за которыми закрепились те или иные имена задолго до появления компьютеров. Списки таких переменных, как правило, приводятся на первых страницах учебников, монографий и некоторых объемных статей, в пояснительных записках к курсовым и дипломным проектам. Специалист, глядя на свою «родную» формулу, может сразу и безошибочно понять, что хранит в формуле та или иная переменная. Переменные при этом могут иметь «национальность»: сравните Din и Dвх, Dout и Dвых (входной и выходной диаметр чего-то там; когда-то давно у нас в пылу борьбы с космополитизмом предписывалось писать не Dвх, а Двх и тд, и этот перегиб до сих пор полностью не изжит в некоторых отечественных машиностроительных стандартах[18]). Но сейчас все чаще и чаще мы стали отказываться от букв кириллицы в формулах не из-за отсутствия должного патриотизма, а по чисто практическим, неполитизированным причинам.
Во-первых, как уже отмечалось выше, формулы для статей и монографий все чаще и чаще «рождаются» в средах математических пакетов, а некоторые из них не позволяют мешать «французский с нижегородским» – вставлять в имена переменные не только буквы кириллицы, но даже и греческие буквы, широко используемые в формулах.
Во-вторых, правила публикации формул в отечественной литературе требуют,
чтобы латинские буквы в переменных были прописаны курсивом, а буквы кириллицы – прямым шрифтом: сравните Dвх и Din (или даже Dvhod[19]). Это задумано для того, чтобы
читатель мог отличать латинские буквы от кириллических, имеющих сходное
написание: А – А, В – В, С – С, Н – Н[20] и
тд. В некоторых математических пакетах (в Mathcad, например) допустимо менять шрифт у отдельных переменных[21], но
ни в одном математическом пакете нельзя форматировать имя переменной, например,
так – саму переменную прописывать курсивом, а ее нижний индекс оставлять
прямым (см. примеры выше). Из-за этого приходиться отказываться от
кириллических слов и сокращений в именах переменных, заменяя их на английские
аналоги: было Dвх
(или даже Двх) стало
Din или Dvhod.
Чисто английские переменные в формулах существенно облегчают научный обмен. Иностранный специалист, совсем не знающий русского языка, может по английской аннотации найти в Интернете профильную русскую статью, просмотреть в ней «английские» формулы, понять, о чем тут идет речь, заказать перевод статьи или связаться с автором. По этой же причине в примерах данной статьи используются не русские, а международные написания единиц измерения физических величин (не м, а m (метры), не Па, а Pa (паскали) и тд – см. раздел 5). Кроме того, электронная версия данной статьи, размещенная на сайте автора, дополнена ее английским переводом, что сделать намного проще имея в оригинале уже «англизированные» формулы. Это можно считать неким вкладом в решение проблемы международного научного обмена.
Отсюда вывод. Если в формулах совсем нет букв кириллицы, то выделение латинских букв курсивом теряет всякий смысл и от этого правила можно и нужно отказаться. Тем более, что многие издательства это правило давно уже игнорируют, понимая в том числе и то, что их читатель довольно грамотный и без особых проблем отличит в формуле русскую букву С (эс), к примеру, от ее английского аналога – буквы С (си). Но в данной статье автор правила «латинская буква – курсив» пока придерживается, в частности, для того, чтобы лишний раз не «дразнить» редакторов и корректоров.
Говоря об именах переменных нужно упомянуть «переменные-иероглифы». Читатель может подумать, что тут речь пойдет о Китае, Японии, Корее и некоторых других азиатских странах[22], о том, как там ученые вставляют в переменные формул свои слова-иероглифы. Но речь пойдет не об этом[23], а вот о чем. Некоторые переменные в некоторых научных дисциплинах «обросли» нижними и верхними индексами, штрихами, «крышечками» и другими специфическими символами и стали из-за этого походить не на сокращения слов или аббревиатуры, а на… иероглифы. Эти «иероглифы» несложно написать карандашом на бумаге или мелом на доске аудитории. При определенном навыке эти «иероглифы» можно ввести в электронную версию статьи (в файл для компьютера), используя упоминавшиеся программы Word Equation или LaTex[24]. Но ввести их в расчет, создаваемый в среде математической программы, очень часто бывает просто невозможно. Такие «иероглифические» имена переменных приходится упрощать – лишать их «многоэтажного» вида, переводить их в линейную (текстовую) форму примерно так, как китайцам, корейцам и японцам приходится упрощать свою письменность, чтобы тексты можно было вводить в компьютер. Из-за этого во многих научных дисциплинах «иероглифические» имена переменных и констант стали обзаводиться своими упрощенными аналогами. Конкретный пример. Можно в текст статьи ввести символ определенного интеграла рисунком[25] или специальным набором, а можно просто набрать на клавиатуре int(f(x), x = 0..1).
В начале многих книг и статей, как мы уже отметили выше, авторы размещают в виде таблицы список переменных, используемых в тексте: первый столбец такой таблицы – имя переменной, второй столбец – единица измерения хранимой в переменной величины (о единицах измерения см. раздел 5) и третий столбец – описание переменной. Если же в книге или статье приводятся фрагменты программ или протоколы решения задач в среде какой-либо математической программы, то в списке переменных может появиться еще один столбец – имя переменной (идентификатор), используемый при компьютерном решении задачи. Иногда этот новый столбец может «вытолкнуть» из таблицы первый столбец с традиционными именами переменных и констант. С экспансией математических пакетов в книги и статьи это «выталкивание» пошло более интенсивно, и мы должны будем постепенно забывать традиционное «иероглифическое» написание не только переменных, но и некоторых математических операторов (см. раздел 7). С другой стороны, разработчики математических пакетов при создании новых версий стараются учитывать устоявшиеся традиции в написании переменных и вводят новые инструменты их форматирования. Так в среде Mathcad с некоторых пор стало возможным вводить в имена переменных верхние и нижние индексы, математические и другие символы. Правда, такую усложненную переменную нужно обрамлять квадратными скобками: [ HCO3- ], [ Dinmin ] и тд.
3. Проблема очередности записей при публикации формул
В книгах, статьях, курсовых и дипломных работах формулы принято публиковать в таком порядке – сначала приводится сама формула с небольшим «заголовком» примерно так:
«Температура идеального газа (T) рассчитывается по формуле:
|
|
( 1[26] )» |
А потом перечисляются переменные, входящие в формулу примерно так:
«где m – молярная масса газа, p – давление газа, v – удельный объем газа[27] и R – универсальная газовая постоянная». Тут перечисляются переменные, входящие в правую часть формулы… Но часто в научных публикациях даются не просто формулы, по которым можно вычислить значение переменной, стоящей в левой части формулы – см. формулу 1, а уравнения (алгебраические, дифференциальные и др.). О такой форме записи формул мы еще поговорим.
Чтобы формула заработала в математических пакетах, необходимо переставить местами саму формулу и список ее переменных, а также ввести в переменные и константы конкретные значения[28]: см. рис. 1 – слепок с экрана дисплея решения задачи (1) в среде Mathcad.
|
|
( 2[29] ) |
Рис. 1. Расчет по формуле в среде Mathcad
«Обвешивание» в книге или научной статье формул числовыми значениями переменных, входящих в формулы, может показаться излишним, если не принять во внимание следующую важную тенденцию в развитии информационных технологий.
Расчеты, выполненные в среде Mathcad и в некоторых других математических программах, можно публиковать в Интернете для интерактивной работы с ними. На рис. 2 отображен сайт с адресом http://twt.mpei.ac.ru/MCS/Worksheets/pv-RT.xmcd[30], зайдя на который можно изменить в прямоугольных окнах исходные данные, нажать[31] кнопку Recalculate[32] и получить новый ответ – численное значение температуры, рассчитанное по формуле (1).
|
|
( 3[33]) |
Рис. 2. Расчет по формуле в Интернете
При публикации формул особенно в электронных изданиях можно рядом с формулой или группой формул поместить ссылку на сайт, где эти формулы можно заставить работать: менять в них исходные данные и получать новые ответы, как это отображено на рис. 2.
Примечание. В переменных расчета, показанных на рис. 1 и 2 , мы, соблюдая вышеотмеченное правило публикации формул, сохранили курсив латинских букв. Из-за этого качество полиграфии несколько ухудшилось. Единицы измерения (а о них речь пойдет ниже в разделе 5) и числа на рис. 1 прописаны прямым шрифтом и выглядят вполне прилично (еще один резон отказаться от правила «латинская буква – курсив», о котором шла речь выше.
При публикации «работающих» формул, как правило, их дублируют с заменой переменных их численными значениями примерно так:
«Энтальпию воды в конце необратимого процесса сжатия ее в насосе h3д вычислим по формуле для расчета относительного внутреннего КПД насоса:
h3д = h2¢ + (h3 – h2¢) / hoiн =121,4 + (133,9 – 121,4) / 0,85 =136,1 кДж/кг» (4)
Такое дублирование ведется для дополнительного контроля, но уже не самой формулы, а правильности численных значений переменных формулы и счета по ним. Предполагается, что человек (некий «сертификатор» расчета), имеющий под рукой калькулятор (арифмометр, логарифмическую линейку, специальные расчетные таблицы, счеты, абак и тд, если идти вглубь истории), может проверить арифметические выкладки, не разыскивая в расчете численные значения переменных, вычисленных ранее.
В среде некоторых математических пакетов также требования стандартов учитываются: там можно дублировать формулы с подстановкой численных значений переменных. Вот пример подобного оформления расчета в среде Mathcad 14 и 15 (рис. 3).
|
|
(5) |
Рис. 3. «Оцифровка» формулы в среде Mathcad
Подобный стиль счета предусмотрен и в некоторых специализированных пакетах – в пакете NormCAD (http://normcad.ru), например, предназначенном для расчетов по российским (машино-) строительным нормам и правилам (СНиПы). Вот пример расчета в среде NormCAD:
«Площадь
арматуры по грани нормальной оси X:
Asx = As1, x
· (nx + 1) + (2 · Aso – As1,
x – As1, y) ·
b / (1 + b) =
=0·(0+1)+(2·0,0008–0–0,000314159)·0,50695/(1+0,50695)
= 0,000432567 м2 (формула (151); п. 3.74, Пособие к СНиП
2.03.01-84).» (6)
Такая «оцифровка» формул была желательна при «ручном» ведении расчетов с помощью калькулятора (арифмометра и тд, см. выше), но стала, как понимает читатель, совершенно излишней при компьютерном счете. Тем не менее, многие устаревшие, но действующие и поныне стандарты оформления расчетов требуют «оцифровки» формул, даже если они велись полностью на компьютере. «По одежке встречают, по уму провожают» – этим правилом руководствуются в различных сертифицирующих организациях, где ваш расчет не примут на проверку, если он оформлен неправильно.
«Оцифровку» расчетных формул требуют многие преподаватели, принимающие типовые курсовые и дипломные проекты в высших и средних технических учебных заведениях. Некоторые преподаватели, принимая от студента такой расчет, кладут около себя калькулятор (чуть раньше они «брали в руки логарифмическую линейку») и проверяют все или по крайней мере некоторые математические выкладки, допуская, что студент тут мог ошибиться, забывая при этом о том, что эти расчеты делал не студент, а компьютер, который не может ошибиться в арифметических выклажках.
Ошибиться тут может студент, выбрав не ту формулу или подставив в нее не то значение, и механическая проверка счета по формулам тут не поможет… Когда-то в МЭИ первые компьютеры стали печатать ведомости на зарплату – колонки цифр с итоговой суммой внизу. Главный бухгалтер МЭИ эти ведомости должен был подписывать. Но прежде чем это сделать он… на счетах проверял правильность числа, стоящего внизу ведомости на зарплату – распечатки компьютера, суммировал все числа. Когда этому главному бухгалтеру говорили, что в итоговой сумме не может быть ошибки, что ошибка может быть только при начислении той или иной зарплаты тому или иному работнику, то ответ был таков – компьютер в случае чего не посадят в тюрьму, а меня посадят, если я подпишу неправильную ведомость… Так и до самого ухода на пенсию этот главный бухгалтер суммировал числа в ведомостях на зарплату на счетах, потом на калькуляторе перед их подписанием… Так и некоторые преподаватели требуют «оцифровки» формул в студенческих расчетах, не понимая, что этим возможную ошибку не выявить…
Процесс «оцифровки», зафиксированный на формулах (4)–(6), требует значительного ручного оформительского труда и не всегда приводит к желаемому результату: к нужному числу знаков в ответе с нужной единицы измерения и т.д. Чтобы «воли были сыты и овцы целы» – чтобы удовлетворить проверяющего расчет и не перегружать себя лишней и трудоемкой работой, можно оформить расчет (см. формулу (4)) так – дать формулу с итоговым ответом, а под ней «распечатать» переменные формулы с нужным форматом числа и с нужной единицей измерения (см. рис. 4).
|
Рис. 4. Формула со списком переменных и их численных значений
«Умный» преподаватель, проверяющий расчет, показанный на рис. 5, видя не совсем или совсем неправильный ответ по формуле, не станет проверять счет по этой формуле. Ему достаточно проверить, какие переменные фигурируют в формуле и какие значения эти переменные имеют. Вот тут то и будет очень полезна распечатка значений переменных анализируемой формулы так, как это показано на рис. 4. Если же возникнет потребность проверки правильности счета по формуле, к примеру, для контроля правильности округления ответа, то около формулы лучше поместить значения переменных с базовыми единицами измерения – см. рис. 4а и сравните его с рисунками 2 и 3.
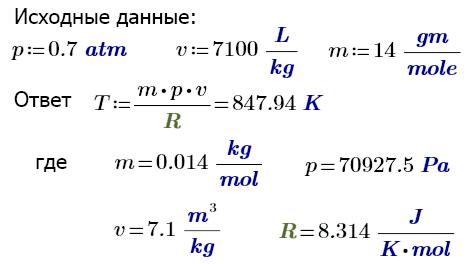
Рис. 4а. Расчет по формуле с переводом единиц измерения к базовым единицам СИ
Другая помощь проверяющему будет заключяться в том, что вблизи формулы размещаются не только значения переменных формул, но и значения некоторых фрагментов формулы. Эта особенность показана на рис. 4b.

Рис. 4b. Расчет по формуле с «распечаткой» значений переменных и фрагментов формулы
Оформление студентом и проверенные преподавателем формулы расчетов могут иметь не только чисто учебное, но и практическое значение за счет перевода расчетов в Интернет и обогащение разного рода справочников. Конкретный пример.
Автор работает в составе группы исследователей, объединенных в Международную ассоциацию по свойствам воды и[34] водяного пара (www.iapws.org), которая готовит и публикует наборы формул (формуляции), по которым предписывается вести расчеты различных параметров этой очень важной природной субстанции, широко используемой не только в быту, но и во всех отраслях промышленности и сельского хозяйства. Обычно такие формуляции публикуются в виде PDF-текста со вставленными в него «мертвыми» формулами. На рис. 5 в качестве примера показан фрагмент одной из таких формуляций, по которой рассчитывается ионное произведение воды Kw – произведение концентрации катионов H+ на концентрацию анионов ОH- в воде. В докомпьютерную эру такие формуляции готовили на пишущих машинках (см. сноску 2), вручную вписывая в них нужные формулы. Теперь же эти формулы уже полностью готовят на компьютере, но до недавнего времени это кардинально дело не меняло.

Рис. 5. Пример формуляции по свойствам воды
С недавнего времени с подачи автора этой статьи и его коллег и студентов [4] подобные формуляции стали публиковаться в виде наборов «живых» интернетовских формул, по которым можно вести соответствующие расчеты. На рис. 6 показан сетевой документ, по которому можно рассчитать ионное произведение воды Kw (вернее, отрицательный десятичный логарифм от этой величины – pKw) в зависимости от температуры и плотности воды.

Рис. 6. Пример «живой» интеренет-формуляции по свойствам воды/водяного пара
Формуляции по свойствам воды и водяного пара, а также других субстанций разрабатываются, утверждаются и публикуются, в том числе и в Интернете для того, чтобы руководствуясь ими можно было создавать программы для компьютерных расчетов, в которых нуждается промышленность, исследовательские и проектные организации, а также учебные заведения. Для ручных же расчетов или приближенных оценок годятся таблицы и графики (о них будет сказано ниже), которые создаются также на основе опубликованных формуляций.
Публикация формуляций в виде сетевых, интерактивных, открытых[35] расчетов (рис. 6) позволяет:
1) просто знакомиться с методикой ведения данного расчета (это, правда, можно и, наверно, даже лучше делать, изучая и традиционные «бумажные», «неживые» PDF-документы – см. рис. 5);
2) проводить конкретные разовые расчеты: менять исходные данные и получать новый результат;
3) создавать и, главное, быстро отлаживать соответствующие программы для компьютеров, имея под рукой не только итоговый ответ (в «неживых» формуляциях такие контрольные итоговые ответы, как правило, приводятся для нескольких расчетных точек), но и все промежуточные данные: на рис. 6 показано, что все формулы данной «живой» формуляции дополнены числовыми ответами.
В самом начале статьи анонсировалась книга [1]. Так вот, все формулы в этом справочнике имеют сетевые, интерактивные, открытые аналоги, разработанные по технологии, отображенной на парах рисунков 1-2 и 3-4.
Авторы других подобных книг с множеством формул вкладывают в книги диски с программами, позволяющими после установки их на компьютере вести расчеты по формулам. Но это устарелая технология, если принять во внимание, что в настоящее время почти все компьютеры имеют выход в Интернет. Но и установка расчетных программ не с приложенному к книге диска, а скачивание их из Сети, полностью не решает эту проблему. И причина этому такая.
Можно отметить следующую тенденцию, которая серьезно изменит жизнь пользователей компьютеров в течение ближайшее время. Тенденция эта заключается в развитии так называемых облачных вычислений (cloud computing) – предоставление пользователям компьютеров удаленных вычислительных мощностей и дискового пространства («облаков»), а также каналов связи. На использование «облачных вычислений» пользователей толкает, помимо прочего, высокие стоимости лицензий программ на отдельные компьютеры, аренды помещений, электроэнергии, а также не в последнюю очередь… тенденции, описанные в данной статье. Пользователю не нужно будет ставить на свой персональный компьютер какие-либо прикладные программы – все можно будет найти в Интернете за умеренную абонентскую плату или совсем бесплатно…
Размещение программ расчета по формулам на выделенном сервере (в «облаках»), а не раздача (дистрибуция) таких программ через диски, приложенные к книге, или через скачивание программ из Сети имеет еще одно важное преимущество. Если в программах обнаружится ошибка в самих формулах или просто «очепятка» в комментариях, то этот промах можно быстро и незаметно исправить. На таком сервере можно также поместить непрерывно дополняющийся список опечаток, допущенных в самой книге (практика, получающая распространение в последнее время). Книгу, от которой тянутся многочисленные «паутинки» ссылок на сервер, можно считать непрерывно «перерабатывающимся, дополняющимся и исправляющимся» изданием.
Особенно много формул содержится в различных задачниках и решебниках[36]. Автор со своими студентами взялся за труд перевести некоторые из них, связанные в первую очередь с энергетикой, в сетевой, интерактивный, открытый формат. При такой «оцифровке» было выявлено множество ошибок и опечаток. И это не только классические ошибки/опечатки (в степени переменной стоит двойка, а не положенная тройка, например), но и некие недомолвки/умолчания, в которых может в конце концов разобраться специалист или даже студент, получающий дополнительные качественные консультации у преподавателя. Но математические пакеты такие недомолвки/умолчания категорически отказываются «извинять», прерывают счет сообщениями об ошибке или выдают ответ, не совпадающий с книжным… И в этом трудно винить авторов, редакторов, а тем более корректоров таких решебников: одно дело вычитать «гладкий» текст, а другое – тщательно проверить формулы, не прибегая к скрупулезному счету по ним. Дело осложняется еще и тем, что в задачниках и решебниках численные ответы формул округляются[37] и эти округленные ответы переносятся в последующие формулы, что может привести и приводит к существенным искажениям в промежуточных и итоговых численных ответах. В математических пакетах в «последующие формулы» переносятся не округленные ответы, вернее, не так сильно округленные ответы (не 574,79°C, а 574,7924189533622°C, вернее не 847.94 К, а 847.9424189533622 К – на «печать» выводятся градусы Цельсия, а сам расчет ведется, естественно, в кельвинах, если вернутся к рис. 1 и 2, что и будет отмечено в разделе 5), что с одной стороны повышает точность расчетов, а с другой, создает проблему разночтений в «живых» и «неживых» («бумажных») решебниках.
Кстати, об округлении ответа. При организации сетевых расчетов желательно давать посетителям сайта возможность задавать число знаков в выводимых числовых ответах (см. пример на рис. 7 – digits).

Рис. 7. Уточнение числа знаков в выводимом ответе
Работа по «оживлению» формул задачников и решебников очень полезна и в таком отношении: выверенные и опубликованные в Сети расчеты приобретают не только чисто учебную, но и практическую ценность, т.к. по ним можно решать конкретные практические задачи. Решебник тут превращается в очень удобный научно-технический справочник.
К особому типу решебников относятся различного рода нормативные документы (строительные нормы и правила – СНиПы, например), где также много формул и которые также можно и нужно «оживить» в Интернете. Что, кстати, уже делается, в том числе и автором данной статьи в отношении некоторых стандартов энергетики. Так на сайте http://twt.mpei.ac.ru/MCS/Worksheets/Thermal/Izol-Trub-Teploset.xmcd читатель может увидеть пример одного из таких «живых» нормативных документов – СНиП по расчету толщины теплоизоляции теплосети[38].
Ведя разговор о нормативных документах, нельзя не коснуться темы сертификации расчетов. Достоверность информации в «бумажных» справочниках в какой-то мере подтверждается солидностью соответствующих издательств с их штатом научных консультантов, редакторов и корректоров. Страницы же Интернета, как правило, отданы на откуп случайным создателям и не подвергаются жесткому редактированию и тщательной корректуре. С другой стороны, автор собрал довольно большую коллекцию опечаток в справочниках весьма солидных издательств, когда вместо, например, 0,02387 стоит 0,02387 (двойка перестала быть нижним индексом, отмечающим повторяющиеся нули), а вместо 27,39 – 72,93 (вероятно, число набрал человек, знающий немецкий язык, на котором говорят не «семьдесят два», а «два и семьдесят», не «девяносто три», а «три и девяносто») и т.п. Такие ошибки практически невозможно выявить при традиционной (визуальной) правке корректур «бумажных» справочников и мы уже это отмечали. Тем не менее, ошибки остаются ошибками со всеми вытекающими последствиями.
Сертификацию расчетных документов, опубликованных в Сети, можно хотя бы внешне проводить двумя способами. Во-первых, можно публиковать в Сети письмо «солидной» организации, где подтверждается правильность размещенных на конкретном сайте расчетов. Во-вторых, можно из сайтов «солидных» организаций делать ссылки на соответствующие расчетные сайты и упоминать об этом на самом расчетном сайте.
4. Проблема «формулы-графики» и «формулы-таблицы»
Особым родом формул (см. сноску в названии статьи) являются графики и таблицы в справочниках, монографиях, научных статьях.
Графики можно разбить на три группы:
1) графики, построенные по известным формулам;
2) графики, построенные после некой статистической обработки (интерполяция, экстраполяция, аппроксимация) дискретных данных (они, как правило, отмечены точками на графике), или графики с утерянными или недоступными формулами, по которым они когда-то были построены;
3) Некие графические зависимости («наброски от руки»), по которым трудно что-либо оценивать, тем более, считать, и которые приведены только для качественной оценки явлений. Такие графики обычно не содержат сетки и чисел по оси ординат, а только обрисовывают некие зависимости: тут функция растет, а тут падает… В литературе, кстати, встречаются и подобные графики «от руки», в которых сделан некий набросок некой зависимости, но по которым практически нельзя и не нужно считать («качественные», но не «количественные» формулы)…
Первые две группы графиков несложно «оживить» в Интернете по технологии, описанной в [2], где этому вопросу уделена специальная глава «График на расчетном сайте». Два примера.
На рис. 8 можно видеть сетевой, интерактивный график, относящийся к первой группе графиков и отображающий зависимость скорости звука в воде/водяном паре от температуры и давления.
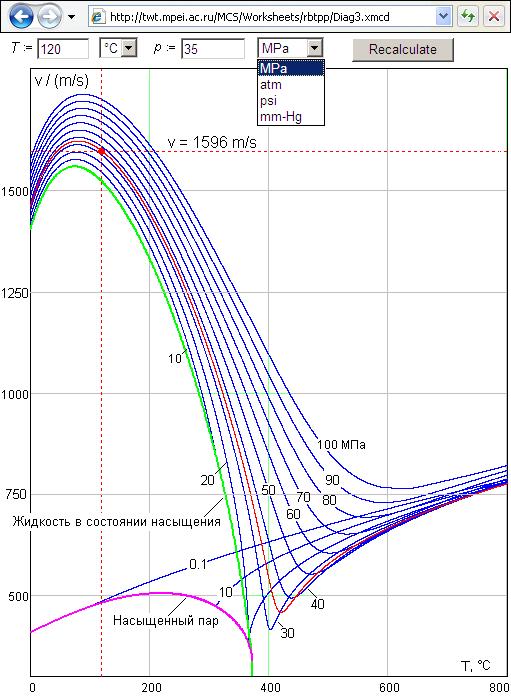
Рис. 8. График зависимости скорости звука в воде/водяном паре от температуры и давления
Изобары, показанные на рис. 8, построены по утвержденной формуляции Международной ассоциации по свойствам воды и водяного пара. Посетитель данного сайта может изменить исходные данные, нажать кнопку Recalculate и получить не только новый числовой ответ (скорость звука в воде/водяном паре), но и новую изобару и новые пунктирные линии, фиксирующие рабочую точку на графике. Это позволяет более глубоко понимать те или иные закономерности в свойствах воды/водяного пара. Есть соответствующие сайты, где строятся не изобары, а изотермы, и даже поверхности в трехмерном пространстве[39]. В Интернете также имеется сайт (http://twt.mpei.ac.ru/MCS/Worksheets/WSP/RegionsAllAxes.xmcd), где показаны все «живые» формулы, по которым строились изобары рис. 8.
Графики второй группы, у которых нет явной аналитической зависимости в виде формул, также можно при определенных усилиях (оцифровка с получением дискретных значений точек на графике, интерполяция или аппроксимация по некоторой зависимости и тд.) опубликовать в Интернете для интерактивного использования. Так в качестве примера на рис. 9 и 10 показана пара графиков: рис. 9 – это сканированный[40] из фундаментального справочника «Физические величины» (М.: Энергоатомиздат, 1991 г. – см. сайт http://twt.mpei.ac.ru/PVHB с «живыми» расчетами из этого справочника) график скорости звука в морской воде в зависимости от ее температуры и солености[41], а рис. 10 – этот же график, открытый в Интернете, с автоматическим построением недостающей изолинии и расчетом скорости звука с фиксацией рабочей точки на графике.
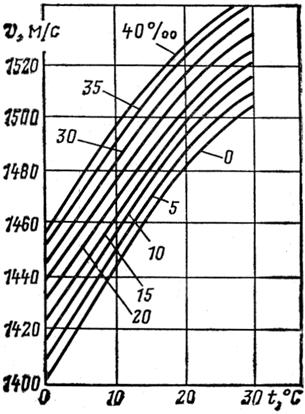
Рис. 9. Пример типичного графика в «бумажном» справочнике
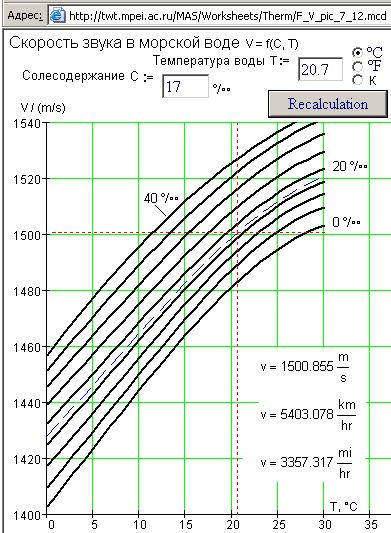
Рис. 10. Пример типичного «живого» графика в Интернете
В справочной литературе встречаются также и разного рода номограммы с инструкциями такого рода: отложите значение первого аргумента на левой шкале, а второго – на правой; соедините точки линейкой и на средней шкале считайте ответ. В номограммах (а на них выросло целое поколение инженеров) «тонет» физика задачи – ее качественная оценка, зато повышается точность расчетов. Выпускались даже нехитрые механические устройства типа логарифмической линейки (см. сноску 60) с «вшитыми» в них алгоритмами расчетов. Такие устройства были особо популярны у штурманов, прокладывающих маршруты морских и воздушных судов до наступления эры бортовых компьютеров и систем глобального позиционирования. Сейчас что-то подобное можно купить в газетных киосках – совместил на двух дисках свой вес и рост и узнал, пора ли переходить на диету… Номограммы также несложно «оживить» в Интернете. Пример одной такой номограммы можно увидеть здесь http://twt.mpei.ac.ru/MAS/Worksheets/Boiler/Th_C_B_Nom_2.mcd.
Научные публикации помимо формул и графиков содержат разного рода таблицы – дискретные значения функций одного, двух или даже трех аргументов. Таблицы также условно можно разбить на группы, но не на три как у графиков, а только на две: таблицы, хранящие дискретные значения, рассчитанные по известным формулам, и таблицы, хранящие эмпирические (опытные) значения, не связанные явно с какими-либо аналитическими зависимостями. Таблицы обеих этих групп можно также «оцифровать» и открыть в Интернете для интерактивного использования. На рис. 11 в верхней его части показан фрагмент таблицы из [1] с дискретными значениями трех функций двух аргументов (давление p и температура T), возвращающих удельный объем (v), удельную энтальпию (h) и удельную энтропию (s) воды/водяного пара.
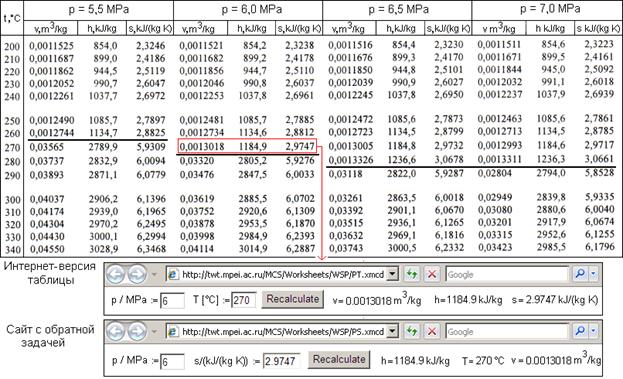
Рис. 11. Пример таблицы свойств воды/водяного пара
Таблицы в век Интернета хороши для… заполнения объема «бумажного» справочника, для увеличения его листинга (см. сноску 42). Но для практической работы таблицы малопригодны. Если, к примеру, приходиться решать прямую задачу – по значениям давления и температуры необходимо найти значение удельной энтальпии (см. таблицу на рис. 11), то путем несложных интерполяций[42] данную задачу можно быстро решить. Но если требуется решить обратную задачу, рассчитать, например, по давлению и удельной энтропии значение удельной энтальпии (очень распространенная теплотехническая задача), то с таблицей, показанной на рис. 11, становится работать весьма сложно. В этом случае существенно поможет Интернет, в котором размещены сайты с расчетами, дополняющими данную таблицу. В нижней части рис. 11 показаны два из таких сайтов, с помощью которых решаются описанные прямая и обратная задачи без каких-либо дополнительных интерполяций и итераций.
Особо следует сказать о маркировке осей графиков (см. рис. 8 и 10) и «шапок»/«боковиков» таблиц (см. рис. 11). Если по оси графика или в «шапке»/«боковике» таблицы отложены значения давления, например, выраженные в мегапаскалях, то в отечественных и зарубежных изданиях можно увидеть следующие маркировки (обозначения): р, МРа или р [MPa] или p / MPa и др. Наиболее правильной (логичной, не таящий лишних умолчаний) можно считать последнюю («американскую»[43]) манеру маркировки осей графиков p / MPa: если мы видим, что точка на оси графика соответствует, например, значению давления (p) 12, то это означает, что p / MPa = 12 или (после умножения левой и правой частей равенства на константу MPa) р = 12 МРа. Такая маркировка на графиках и таблицах особо полезна, если в единицах измерения присутствуют множители. Рассмотрим, например, график, где по оси ординат отложено не давление (см. выше), а динамическая вязкость, которую часто измеряют микропаскалями, помноженными на секунду: μ / (10-6 Ра s) = 100 → μ = 100·10-6 Ра s → μ = 0.0001 Ра s[44]. Тут все логично: динамическая вязкость равна одной десятитысячной паскаля, умноженного на секунду или ста микропаскалям, помноженным на секунду – эту величину можно вставлять в расчет и считать дальше. Но в отечественных изданиях на таких графиках и в таблицах можно видеть не только правильную запись: μ · 106, Па с или μ, 10-6 Па с, где под запятой подразумевается знак деления (практичные американцы его не подразумевают, а явно прописывают – см. выше), но и ошибочные: запятую ставят не на нужном месте (μ, 106 Па с) или путают знак порядка (μ · 10-6, Па с). «Американская» манера надписей, повторяем, в этом смысле более практична – тут явным образом ставится знак деления, а не его малоизвестный «псевдоним» – запятая[45]. Правда, и тут бывают неточности. На осях «американского» графика можно увидеть надпись T / °C или Т / °F (относительные температурные шкалы Цельсия или Фаренгейта). Здесь символ / означает уже не деление, а более сложную зависимость, включающую сдвиг по константам 273,15 К (кельвины) или 459.67°R (градусы Ренкина). В этом случае правильнее писать не T / °C или Т / °F, а T, °C или Т [°F], подразумевая под запятой или квадратными скобками символ этой «более сложной зависимости». Так, например, были оформлены графики на рис. 8 и 10. Символ / будет означать деление в случае маркировки T / K или Т / °R – абсолютные температурные шкалы Кельвина (кельвины) или Ренкина.
5. Проблема формул с переменными, хранящими физические величины
Вернемся к формуле (1) и к тексту, его поясняющему. Очень часто в книгах и статьях можно встретить формулы, где дополнительно отмечены единицы измерения величин[46], фигурирующих в формулах, примерно так:
«Температура (T, кельвины) идеального газа рассчитывается по формуле:
|
|
( 3[47] ) |
где m – молярная масса газа (г·моль-1), p – давление газа (Па), v – удельный объем газа (м3·кг-1) и R – универсальная газовая постоянная (8,314472 Дж·моль-1·К-1).»
Эти дополнительные указания на единицы измерения могут показаться лишним: если названа физическая величина, то незачем напоминать читателю, какими единицами она измеряется. Но…
Как известно, все формулы по своей сути и отчасти по своему внешнему виду, а также описанию делятся на две группы: формулы, связывающие физические величины и формулы, связывающие физические величины с фиксированными единицами их измерения. Первая группа формул (F = a · m, E = m · c2 и тд и тп[48]) описывает наши теоретические представления об окружающем мире. Вторая группа формул, так называемые эмпирические формулы, описывают экспериментальные данные, пока не подвергнутые более-менее глубокому теоретическому анализу, убирающему у формул «унизительное» прилагательное «эмпирическая»[49]. Описание переменных формулы (3) включает в себя перечисление и единиц измерения. Следовательно, по этому формальному признаку данную формулу можно считать эмпирической. Но это, конечно, не так – это полноценная «теоретическая» формула, вытекающая из уравнения Клайперона – Менделеева[50] р · v = m · R · T [51]. Формулу (3) можно считать псевдоэмпирической. Такие формулы, отягощенные упоминанием единиц измерения и дополнительными коэффициентами, очень часто можно встретить в научно-технической литературе. Дело в том, что если вернуться к формуле (3), то можно отметить то, что молярную массу принято измерять не в килограммах[52] на моль, как это требует Международная система единиц (СИ), а в граммах на моль, к чему мы все привыкли и как это зафиксировано в различных физических и химических справочниках. В формуле же (2) коэффициент 1000 (грамм в килограмме) отсутствует. Почему?! Современные математические пакеты, в частности Mathcad и Maple, работают не просто с величинами (это умеют делать языки программирования и табличные процессоры), а с физическими величинами[53] – массой, объемом, количеством вещества, температурой и тд. При расчетах эти пакеты сами сделают соответствующие дополнительные пересчеты единиц измерения, что и отображено в примере, показанном на рис. 2[54]. Более того, эти пакеты ведут контроль размерностей и не позволяют, грубо говоря, складывать метры с килограммами, что очень способствует более быстрому и, главное, безошибочному вводу формул.
Коэффициент 1000 в формуле (3) нетрудно «расшифровать» – это, повторяем, 1000 грамм в одном килограмме. Но в других подобных формулах такие коэффициенты, позволяющие задействовать в расчетах небазовые или устаревшие единицы измерения, «расшифровывать» бывает намного труднее. Что такое число 3,6, фигурирующее в некоторых формулах?! Это 3600 секунд в часе и 1000 кг воды в кубическом метре[55]. Еще труднее понять суть таких коэффициентов, если в формулах предписывается использовать единицы измерения, некратные основным (не паскаль, а атмосферу, например) или «заокеанские» единицы (не литры, а баррели, например, если вспомнить цену нефти). Нередко в подобные коэффициенты прячут некоторые константы с благими намерениями облегчить расчет . Типичный пример. Во всех справочниках и учебниках по теплотехнике сказано, что удельный расход топлива на электростанции (b, г/кВт∙ч) вычисляется по формуле b = 123/η, где η – это КПД электростанции, выраженный в абсолютных единицах. Если же эта величина будет выражена в процентах, то формула будет выглядеть несколько иначе: b = 12300/η. Пример: η = 0,32 b = 123/η = 123/0,32 = 384,4[56] г/кВт∙ч. (η = 32 b = 12300/η = 12300/32 = 384,4 г/кВт∙ч): электростанция с КПД 0,32 (32%) сжигает 384,4 грамм условного топлива на выработку одного киловатт-часа электроэнергии. Если же кто-то попробует формулу b = 123/η (b = 12300/η) ввести в Mathcad и посчитать по ней с привлечением механизма единиц измерения, то ответ получится в лучшем случае безразмерным (п. 1 на рис. 12), а в худшем – ошибочным (п. 2).
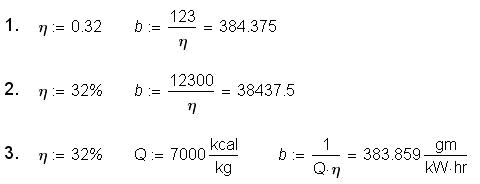
Рис. 12. Расчет в среде Mathcad эффективности электростанции
Дело в том, что нормальная, «физическая», неупрощенная формула для расчета расхода условного топлива выглядит так: b = 1/(Q·η), где Q – это теплота сгорания условного топлива, принятое и легко запоминающееся значение которой равно 7000 ккал/кг (антрацит хорошего качества). Но при переходе на СИ решили, что специалистам, а тем более студентам будет трудно переводить калории в джоули, часы в секунды, килограммы в граммы, и заранее сделали такой пересчет, получив при этом опять же запоминающийся коэффициент 123 (или 12300). В настоящее время, как мы уже отметили, пересчет единиц измерения берут на себя математические программы и в справочники желательно вернуть первозданную формулу b = 1/(Q·η) – см. п. 3 на рис. 12[57], убрав упрощенную b = 123/η. А еще лучше иметь в справочниках две подобные формулы, отмечая при этом, что первая формула (b = 123/η) годится для ручного счета или счета с помощью «нефизических» программных средств (калькулятор, языки программирования, электронные таблицы), а вторая (b = 1/Q/η) – для счета в средах современных «физико-математических» программ со встроенными единицами измерения.
Ошибки, связанные с неправильным использованием единиц измерения издавна сопровождали все сферы человеческих отношений. Например, Петр I в письме князю Куракину (1714 г.) укорял последнего: «... присылали вы роспись подрядным кораблям, которым написана пропорция амстердамскими футами, а я к вам всегда писал, чтоб английскими, о чем зело удивляюсь, для чего сие пренебрегли, ибо убыло в длину более 10 фут, а также и в ширину». В наш же век, в век техногенных катастроф последствия и наносимый ущерб от такого рода ошибок могут быть более значительными.
Два других более свежих примера.
Так, самолет Boeing 767, принадлежащий канадским авиалиниям, 23 июля 1983 года совершал полет из Монреаля в Эдмонтон. На полпути, на высоте 12 500 м, по причине полного расхода топлива лайнер был вынужден совершить аварийную посадку на заброшенном военном аэродроме в местечке Гимли (Gimli). Причиной аварийной ситуации стала ошибка командира, неправильно рассчитавшего массу топлива, необходимого для перелета. В то время авиация Канады переходила с британской метрической системы (в которой объем измеряется в галлонах, а масса в фунтах) на международную метрическую систему SI (литры и килограммы, соответственно). Для пересчета массы потребного топлива следовало показания топливомера (в литрах) умножить на соответствующее значение плотности, чтобы получить килограммы. Ошибка состояла в том, что вместо правильного значения плотности (измеряемого в кг/л), командир использовал старое значение (измеряемое в фунтах/галлон). В результате самолет был заправлен только половиной необходимого топлива, что и привело к аварийной ситуации.
Похожая ошибка привела к неудаче и при полете американского спутника Mars Climate Orbiter (MCO). Mars Climate Orbiter был запущен 11 декабря 1998 года на РН Дельта-2. Аппарат прибыл к Марсу через 9 месяцев, 23 сентября 1999 года. В расчетное время на высоте 193 км аппарат включил двигатели на торможение. Через 5 минут MCO ушел за Марс и больше никаких сигналов с него не поступало. Из анализа данных со станций слежения было установлено, что аппарат прошел над поверхностью на высоте всего 57 км вместо расчетных 140 км и попросту сгорел в атмосфере (стоимость аппарата 125 млн. долларов). Столь большое отклонение было вызвано ошибкой специалистов, готовивших миссию: при расчетах тормозного импульса одна из групп использовала британские единицы измерения (фунт-сила), а другая — метрические (ньютон).
Можно упомянуть еще одну инженерную ошибку, ставшую почти что легендой, но связанную не с самими единицами измерения, а с относительными шкалами измерения. Строили мост через Рейн. С одного берега это делали немцы, а с другого швейцарцы (у тех и у других, заметим, очень высокий уровень технической культуры). Когда пролеты моста стали соединяться на середине реки, то оказалось, что разница в их высотах составила чуть ли не полметра. Причина ошибки была в том, что в Германии строительный стандарт нулевой высоты – это уровень Северного моря, а в Швейцарии – Средиземного[58].
Любой специалист в любой области науки и техники может привести множество примеров подобных ошибок и казусов, связанных с неправильным оперированием единицами измерения в формулах. Отход от ручных расчетов и переход на компьютерные «безразмерные» языки программирования в какой-то степени решает эту проблему.
В свое время (третья четверть XX века) при повсеместном переходе на СИ были «вычищены авгиевы конюшни» – в справочниках и учебниках при их переиздании или новом написании все формулы были переделаны так, чтобы в них, не дай бог, не «всплыли» калории, атмосферы, килограммы-силы и прочие устаревшие, но, тем не менее, широко используемые единицы измерения. Повсеместное распространение математических пакетов, умеющих не только манипулировать числами, но и пересчитывать при этом единицы измерения, требует, чтобы мы еще раз почистили эти «конюшни», привели в порядок формулы – дали, например, их разное написание, учитывающее и традиционную и современную технологию счета, дополнили такую раздвоенную формулу[59] ссылкой на сайт Интернета, где по ней не только можно посчитать, но и построить, если понадобиться, графики, а также получить дополнительную информацию, не вошедшую в компактное «бумажное» издание.
Сейчас в отечественных научно-технических кругах остро ставится вопрос об издании новых или просто о репринтном переиздании «старых, добрых, советских» справочников. Речь даже заходит о переиздании справочника (таблиц) функций Бесселя?! Критики же тут говорят с поддевкой – а давайте еще и таблицы Брадиса[60] переиздадим! «Поддевка» тут в том, что в настоящее время у всех тех, кому такие таблицы нужны, есть под рукой как минимум калькулятор (научный калькулятор с вшитыми в них не только элементарными функциями (таблицы Брадиса), но и функциями Бесселя и другими специальными), а как максимум – персональный компьютер с выходом в Интернет.
Справочники переиздавать и издавать, конечно, нужно. Но при этом необходимо учитывать современные реалии, в частности ситуацию, описанную в данной статье, когда в «бумажном» справочнике от формулы (графика, таблицы) можно через соответствующие ссылки перейти к их «живым» аналогам в Интернете. Но тут встает «крамольный» вопрос – а нужны ли тогда вообще традиционные «бумажные» справочники?! Да, нужны, но в ином формате и исполнении!
Математические пакеты, умеющие правильно работать с физическими величинами, поднимают еще один частный вопрос. В свое время при переходе на СИ издательства и редакции журналов перестали принимать рукописи, где использовались не «сишные», но, тем не менее, до сих пор широко используемые единицы измерения. Особенно больно эта ломка шла в научно-технических кругах, где в ходу фунты, футы и прочие «заокеанские» единицы. Да и у нас в России и во всей Европе есть свои «футы-фунты»: атмосферное давление, к примеру, мы никогда не научимся оценивать в паскалях, вернее, в гектопаскалях[61], а всегда будем тут оперировать миллиметрами ртутного столба. Резюме! Физико-математические пакеты позволяют отойти от жесткого правила, предписывающего использовать в статьях и книгах только единицы СИ. Мы этим возможным будущим послаблением уже воспользовались – на рис. 1 и 2 давление газа было введено в атмосферах физических, а не в мегапаскалях, как этого может потребовать редактор. На рис. 8 можно видеть, что посетитель сайта, желающий узнать скорость звука в воде/водяном паре, имеет возможность ввести значение давления, используя на выбор разные единицы измерения: мегапаскали, атмосферы, фут-силы на квадратный дюйм (psi) или мм ртутного столба (mm-Hg). Такой же выбор предоставляется при вводе температуры: шкала Цельсия[62], кельвины, шкала Фаренгейта, градусы Ренкина или шкала Реомюра[63].
6. Проблема эмпирических формул
А теперь поговорим о «правильных» эмпирических формулах.
Работа с одной из них отображена на рис. 13. В справочниках по теплотехнике можно, например, встретить такую формулу и ее описание:
«Коэффициент теплоотдачи (α, ккал∙м-2∙ч-1∙К-1) высчитывается по формуле:
|
α = 3·р0.15·q0.7 |
( 4 ) |
где p – давление (атмосферы
технические, кгс∙см-2) и q – тепловой поток (ккал∙м-2∙ч-1).»
Внешним признаком эмпирических формул часто являются дробные значения показателей степеней как в нашем случае. Из-за этого ввод в Mathcad-расчет выражения α = 3·р0,15·q0,7 дает неправильный ответ с «непонятной»[64] единицей измерения – kg0.85 · m-0.15 · s-2.4 (см. п. 1 на рис. 13).

Рис. 13. Работа с эмпирической
формулой в среде Mathcad
Эмпирическая формула, по которой ведется расчет коэффициента теплоотдачи, была получена после статистической обработки экспериментальных данных. При публикации эмпирических формул всегда четко отмечается, в каких единицах должны быть исходные величины и в каких единицах будет дан ответ. Этими единицам измерения необходимо дополнить эмпирическую формулу. На рис. 13 в п.п. 2 и 3 так и было сделано: переменные формулы были поделены на приписанные им единицы измерения, сама формула была умножена на приписанную ей единицу измерения.
Отсюда вывод. Если в справочнике нужно поместить эмпирическую формулу и думать при этом о том, что ее будут «оживлять» с помощью физико-математических пакетов, то нужно не просто упомянуть в описании формулы, с какими единицами она должна работать, а непосредственно вставить эти единицы в саму формулу, как это показано на рис. 13. Обновлять такую формулу – пересчитывать для нее новый коэффициент, учитывающий современную систему измерений (а это пытаются делать в новых справочниках), нет необходимости. Более того, устаревшие и/или «иноземные» единицы измерения в эмпирических формулах несут некий дух времени их создания и колорит страны, где они возникали. Литературная аналогия. В беллетристике часто можно встретить единицы измерения. Иногда они «всплывают» даже в названиях рассказов, повестей, романов: «451° по Фаренгейту», «20 000 лье под водой» и т.д. Тут принято не переводить (фаренгейты в цельсии) и не обновлять (лье в километры) при переводе текстов, чтобы опять же не потерять «дух времени и места» описываемых событий.
7. Проблема «математические операторы и операторы математических программ»
Мы в конце раздела 2 коснулись проблемы различного написания математических операторов в справочниках и в средах математических программ.
Одна из причин популярности Mathcad заключается в том, что пользователь может вставлять в документы математические операторы в тех их написаниях, к какими он привык, изучая математику в школе или вузе. Благодаря этому Mathcad-документ максимально похож на лист с математическими выкладками, написанными от руки или созданными в среде какого-либо текстового процессора – редактора математических выражений[65].
С другой стороны, наш стиль написания математических выражений «на бумаге» («общепринятая математическая нотация») тоже меняется под воздействием математических пакетов. Некоторые, правда, видят в этом просто снижение общего уровня математической культуры. Другие же считают, что это связано с неизбежным процессом «компьютеризации» математики. Так в настоящее время квадрат синуса все чаще и чаще стали записывать не как sin2x, а как sin(x)2 или (sin x)2 или (sin(x))2 или (sin(x))^2 или (sin(x))**2, не полагаясь на принцип умолчания. Другой пример. На рис. 6 можно увидеть формулу Q = ρ · e(…), где константа e (основание натурального логарифма) возводится в степень, представляющую собой некий многочлен. Чтобы здесь не возникло ошибки и разночтений, оператор возведения в степень лучше заменить на функцию exp: Q = ρ · exp(…). И таких примеров влияния компьютера на эволюцию написания математических выражений (наших с вами формул) можно привести множество: 10x заменяют на ext(x), |x| – на abs(x) и тд и тп. С другой стороны, выражения exp(…), ext(…), abs(…) и тд могут восприниматься не как функции exp, ext, abs и тд, а как переменные exp, ext, abs и тд, перемноженные на выражение, заключенное в скобки. Поэтому, то во всех формулах данной статьи знак деления прописан явно точкой, а не пробелом или даже отсутствием пробела.
Особо следует коснуться математического символа = (равно), присутствующего почти во всех формулах справочников. В математических пакетах этот символ разбивается на несколько самостоятельных, имеющих собственное написание и значение.
Во-первых, если говорить о пакете Mathcad, то, например, такая простая запись как р = 12 МПа может иметь два толкования. Во-первых, эта запись означает, что переменной р присваивается численное значение давления в 12 магапаскалей. В среде Mathcad эта операция выглядит так р := 12 МРа (см. третью строку рис. 12). Во-вторых, выражение р = 12 МПа может означать (а в среде Mathcad и означает), что тут выводится на дисплей численное значение переменной р, рассчитанное ранее[66] (вывод «на печать» результата расчета). Символ «=» может иметь и третье значение – означать инфиксный булев оператор «равно», разделяющий левую и правую части различных уравнений. Например, знаменитую формулу F = a ∙ m (второй закон Ньютона) можно, во-первых, считать выражением, по которому рассчитывается значение силы (F := a · m) при известных значениях ускорения (a) и массы (m), а во-вторых, можно считать уравнением F = a ∙ m [67], в котором численно или аналитически можно определить значение одной переменной (F, a, или m), если известны значения двух других. Отсюда вывод. Если в справочниках отображается некий реальный расчет, то с символом «=» нужно обходиться весьма деликатно – воспринимать его в разных случаях по-разному: символ присваивания, символ «вывод на печать» или символ «булево равно».
Математические пакеты требуют реформирования написания и некоторых других символов математики, принятых в тех или иных научных дисциплинах, сведения по возможности этих символов к одному «компьютерному» написанию. Поясним этот тезис конкретным примером, связанным также с теплотехникой – с формуляцией по теплофизическим свойствам льда.

Рис. 14. Фрагмент формуляции по теплофизическим свойствам льда
На рис. 14 показан фрагмент формуляции в виде PDF-файла по теплофизическим свойствам льда. В данной формуляции предписывается, как по значению удельной свободной энергии Гиббса (функция двух аргументов: давление и температура) через взятие частных производных по давлению или температуре можно рассчитать следующие параметры льда: плотность (ρ), удельную энтропию (s) и удельную изобарную теплоемкость (cp). При этом используется особая нотация частной производной, принятая в термодинамике более века назад. Эта нотация довольно путанная: в одном случае (см. на рис. 14 столбец Property – свойство) нижний индекс означает, что частная производная берется именно по переменной, указанной в индексе, а в другом (столбец Relation – соотношение), что эта переменная наоборот является константой. В других научных дисциплинах да и в самой термодинамике можно встретить и другие нотации оператора взятия производных. Чтение таких выражений осложняется и тем, что у функции при взятии их производных не перечисляются аргументы: записано просто g, а не g(T, p). Это можно отметить и в отношении других математических операций и функций[68]. В этом разнобое кроется причина многочисленных ошибок не только у студентов, изучающих термодинамику, но даже и у опытных специалистов.
Математические пакеты, как мы уже отметили, не могут «терпеть» таких умолчаний и разночтений. Но правильнее сказать так. Математические пакеты при всей своей гибкости и «настраиваемости»[69] не могут учесть всех нюансов и различий в написании одного и того же математического оператора в разных научных дисциплинах. Поэтому пользователям приходится подстраиваться под возможности математических пакетов. На рис. 15 представлен открытый, интерактивный, сетевой вариант формуляции по свойствам льда, где использована нотация производной, встроенная в Mathcad и понятная всем пользователям.

Рис. 15. Интернет-формуляция по теплофизическим свойствам льда
Как видно из рис. 15, Mathcad имеет четко установленный символ взятия частных производных, не требующий указания констант. Такой стиль написания математических операторов может и должен перейти не только в формуляции, но и в современные учебники и справочники.
Литература[70]:
1. Александров А.А., Орлов К.А., Очков В.Ф. Теплофизические свойства рабочих тел теплоэнергетики. М.: Издательский Дом МЭИ, 2009
2. Кондакова Г.Ю., Копылов А.С., Орлов К.А., Очков А.В., Очков В.Ф., Чудова Ю.В. Справочное издание «Интернет-версия справочника Теплоэнергетика и теплотехника. Инструментальные средства создания и развития» (грант РФФИ 07-08-07003). Издательский дом МЭИ, 2007
3. Очков В.Ф. Mathcad 14 для студентов и инженеров: русская версия, БХВ-Петербург, 2009
4. Alexandrov A.A., Ochkov V.F., Orlov K.A.
Steam Tables and Diagrams on Mathcad Calculation Server for Personal Computers,
Pocket Computers and Smart Phones // Proceedings of the 15th International
Conference of the Property of Water and Steam, Berlin/Germany, September 7–11,
2008
5. Очков В.Ф., Яньков Г.Г. Математические пакеты и проблема передачи знаний // Вестник РФФИ, № 4 (60), 2008
6. Очков В.Ф. Теплотехнический справочник в Интернете // Новое в российской электроэнергетике, № 5, 2005
7. Очков В.Ф. Математические пакеты и сетевой интерактивный теплотехнический справочник: проблемы и решения // Теплоэнергетика, № 6, 2006



