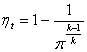Открытые,
интерактивные, сетевые решебники: проблемы и решения
В.Ф.Очков*, Colin Selleck**,
Sasha Gurke***
*Московский энергетический институт (ТУ)
**
Binghamton
University (New York, USA)
***
Knovel Corp. (New York, USA)
Ключевые слова:
теплотехника, Интернет, справочники, задачники, решебники, облачные вычисления
Аннотация: Приводятся
результаты работ по созданию открытых, интерактивных, сетевых решебников и
справочников в области теплотехники, тепло- и электроэнергетики. Обсуждаются
методические и технические проблемы этого нового направления стыка энергетики и
информационных технологий.
Abstract: Development of public,
interactive online calculators and references for HVAC and thermal and electric
power engineering is reviewed. Methods and technical issues in this new field
at the junction of energy and information technologies are discussed.
…семьдесят восемь, по тридцати копеек за душу, это будет... – здесь герой наш одну секунду, не более, подумал и сказал вдруг: – это будет двадцать четыре рубля девяносто шесть копеек – он был в арифметике силен.
Н.В.Гоголь «Мертвые души»
Поэма Н.В. Гоголя, откуда взят эпиграф, изучена исследователями творчества великого писателя вдоль и поперек. Вот только арифметическая ошибка, вкравшаяся в поэму (см. эпиграф), осталась почему-то без комментариев. А, ведь, если перемножить 78 на 0,30, то мы получим 23,40, но никак не 24,96.
Поиск и разбор математических задач из художественной литературы – это одно из хобби одного из авторов [1-2]. Если же при этом такую задачу удается разобрать на занятия по информатике, то это может способствовать появлению или возрождению у студентов интереса к литературе без чего нельзя сформировать полноценную личность. А это, как известно, одна из главных задач высшей школы [3].
Арифметические, а также методические ошибки и опечатки, увы, можно найти и в справочниках, учебниках, задачниках и решебниках[1], где теоретический материал дополняется разбором конкретных практических задач с арифметическими выкладками, с подстановкой численных значений переменных в формулы. Эти ошибки, к сожалению, остаются незамеченными как самими авторами, так и рецензентами, редакторами и корректорами, работавшими над изданием. Такие ошибки, увы, «кочуют» из издания в издание – «исправленные, переработанные и дополненные». И только пропуск этих задач через процедуру «оживления», о которой будет рассказано ниже, высвечивает такие ошибки и позволяет их не только исправить, но и задуматься об их природе.
В настоящее время бурно развиваются технологии публикации в Интернете расчетных документов[2], созданных в средах математических программ [4-5]. Такие документы публикуются не только для просмотра (это делалось уже давно), но и для полноценного счета по ним, когда можно изменить исходные данные, нажать специальную кнопку и получить не только ответ в виде числа и точки на графике, но и все промежуточные результаты расчета с показом соответствующих формул и численных значений задействованных в формулах переменных. С помощью таких сетевых, интерактивных, открытых расчетных документов можно не только изучать те или иные методы решения конкретных задач (это можно делать и без компьютера, открыв обычный, «бумажный» учебник, задачник или решебник), но и преследовать чисто практическую цель – считать, получать новые ответы при новых исходных данных.
Самый популярный математический пакет для инженерно-технических расчетов и расчетов учебной направленности – это Mathcad [5]. Так сложилось по раду причин, главные из которых такие: низкий порог вхождения в эту программную среду, наличие русскоязычной версии и обширной русскоязычной литературы, а также сайтов поддержки (www.mathcad.ru, например). Кроме того, созданные в среде Mathcad расчеты содержат формулы, которые по внешнему виду ничем не отличаются от формул «бумажных» учебников, задачников и решебников. Имена переменных в среде Mathcad полностью совпадают с теми написаниями, которые закрепились в той или иной научной дисциплине задолго до появления компьютеров. Все это способствует максимальной открытости Mathcad-расчетов. Кроме того, созданные в среде Mathcad расчеты можно после минимальной доработки опубликовать в локальной или глобальной компьютерной сети по технологии Mathcad Application Server – MAS [5].
Один из авторов в течение многих лет, используя технологию MAS, опубликовал в Интернете большое количество расчетных документов, связанных в первую очередь с энергетикой – см. сайт www.vpu.ru/mas. В этом этому автору помогают студенты МЭИ и других учебных заведений, для которых такая работа – прекрасный способ изучить ту или иную учебную дисциплину и одновременно серьезно поработать на компьютере. Но тут возникают «проблемы и решения», некоторые их которых мы попытаемся высветить в этой статье на примере одной несложной задачи, взятой из [6][3].

Рис. 1. Отсканированный фрагмент задачи по гидравлике
Не будем обращать внимание на опечатках в задаче (отсутствие знака равенства после переменной hвп.p в формуле Борда, например), а остановимся на другом.
В задаче, показанной на рис. 1, фигурирует переменная ω1, о которой ничего не сказано в самом описании задачи. Ее смысл (площадь сечения трубы) можно понять, только проанализировав числа, подставленные в формулу для определения скорости воды v1 в трубе диаметром d1. Можно, конечно, полистав учебник, найти в нем, что такое ω – «пи де квадрат на четыре». Эту особенность (фигурирование в задаче переменных, о которых ничего не сказано в самой задаче) очень часто можно заметить в учебниках, задачниках и решебниках. Многие преподаватели считают это даже неким полезным методическим приемом, оправдывающим такое умолчание, – пусть, мол, студент полистает эту или другую подобную книгу или «залезет» в Интернет и найдет ответ на возникший вопрос. Но скорее всего тут перед дробью с численными значениями переменных авторы учебника [6] просто забыли вставить более развернутую формулу Q∙4/(π∙d12). Или просто авторы немного злоупотребили принципом умолчания и опустили описание переменной ω1, смысл которой для них совершенно ясен, но далеко не ясен для учащихся.
С «лишней» переменной ω1
в расчете, показанном на рис. 1, разобрались – идем дальше.
Если на калькуляторе подсчитать, чему равно 0,03∙4/(3,14∙10-2), то мы получим 3,82 , но не 3,84. Это, кстати, косвенно отмечено в самой задаче: на рис. 1 в формуле для расчета v2 (скорость воды во второй трубе) фигурирует уже число 3,82, а не 3,84. Но потом при расчете значения hвп.p (потеря напора при внезапном расширении трубы) опять «всплывает» число 3,84. Все это можно считать мелкими придирками, если бы не одно обстоятельство. Эти задачи разбирают учащиеся и студенты, которые, как правило, по умолчанию полагают, что «преподаватель всегда прав» и не может ошибаться. Некоторые добросовестные и дотошные студенты, а таким в первую очередь адресованы наши учебники, задачники и решебники, начинают искать какой-то тайный смысл в таких отклонениях, отвлекаясь от сути задачи. Если при этом «контрольный расчет» будет вестись не вручную, а на компьютере, то расхождение в том, что написано в книге и получено на компьютере может быть весьма значительным – смотрите рис. 2 и сравните его с рис. 1.

Рис. 2. Открытый в Интернете фрагмент задачи по гидравлике
На рис. 2
показана страница Интернета (http://twt.mpei.ac.ru/GDHB/OGTA.html) с нашим «ожившим»
гидравлическим расчетом, где зафиксированы неточности, приводящие к более чем
трехпроцентной ошибке (ответ – потеря напора 0.23 m,
а не 0.22 m)[4]. Можно, конечно возразить, что сами
исходные данные (расход воды и диаметр труб) имеют значительную погрешность, да
и сама формула Борда весьма неточная. Но еще раз упомянем «добросовестного
и дотошного» студента, который попытается разобрать задачу, решить ее на
компьютере, закрепляя тем самым полученные теоретические знания?!
Дело осложняется еще и тем, что в справочниках,
учебниках и решебниках промежуточные численные ответы округляются и эти
округленные значения переносятся в последующие формулы, что может привести и
приводит к существенным искажениям в итоговых ответах. В
математических пакетах в последующие формулы переносятся не округленные ответы,
вернее, не так сильно округленные ответы, что с одной стороны повышает точность
расчетов, а с другой – создает проблему разночтений в компьютерных и «бумажных»
учебниках, задачниках и решебниках.
Все это нужно учитывать авторам новых или
переиздаваемых учебников, задачников и решебников.
Работа по «оживлению» формул решебников очень
полезна и в таком отношении: выверенные и опубликованные в Сети расчеты
приобретают не только чисто учебную, но и практическую ценность, т.к. по ним
можно решать конкретные практические задачи. Решебник тут превращается в очень
удобный научно-технический справочник.
Операция «оживления» расчетов по технологии MAS или по другой подобной информационной технологии (IT), позволяет, повторяем, подвергнуть эти методические материалы серьезному научному редактированию и тщательной корректуре. Это, во-первых, но не в главных. Другие существенные моменты:
1) Калькуляторы и компьютеры сыграли с расчетами злую шутку – из расчетов были выдавлены единицы измерения. Пакет Mathcad, оборудованный инструментарием работы не просто с величинами (числами), а с физическими величинами (длина, масса, время, давление, мощность и т.д. [2, 5]) намного упрощает расчеты и ведет дополнительный их контроль. Если вернуться к задаче, показанной на рис. 1 и 2, то можно заметить, что расход воды, как правило, измеряется в кубических метрах в час, а не в секунду, а диаметры труб в миллиметрах, а не в метрах. С компьютерами и калькуляторами мы переложили на плечи машины заботу о счете. С появлением математических пакетов «на плечи» компьютеров легла дополнительная рутинная работа по пересчету небазовых единиц измерения (час, миллиметр, лошадиная сила и т.д.) в базовые единицы СИ (секунда, метр, ватт и т.д.). Ведь, как не пытаются методисты вузов и научные редакторы издательств полностью изгнать внесистемные и даже вспомогательные единицы измерения из расчетов, они в расчетах останутся. Атмосферное давление, к примеру, мы всегда будем измерять в миллиметрах ртутного столба, а не в абстрактных и непонятных паскалях или даже в гектопаскалях. В США, например, ученые которых сейчас задают тон во многих областях науки и техники, еще долго, а может быть и всегда, будут использоваться фунты и футы, а не килограммы и метры…
2) Решение задач очень часто сводится
к решению систем алгебраических, дифференциальных, интегро-дифференциальных и прочих
уравнений. Здесь часто составителям задач для решебников приходится идти на всяческого рода допущения,
упрощения и другие «методические» хитрости, чтобы свести решение задач к
последовательному счету по набору несложных формул. Ищется и
приводится, например, аналитическое решение системы уравнений – точное, но
чаще упрощенное с некоторыми оговорками и допущениями, с исключением
нелинейностей, например.. Если же при этом не приводится и не анализируется
сама система исходных уравнений (математическая модель), а только дается набор
готовых формул, составляющих решение, то студент не до конца будет понимать
суть задачи. Математические пакеты, оборудованные мощными численными и
аналитическими (символьными) средствами решения систем уравнений, позволяют по-новому
формулировать задачу, обращая при этом основное внимание на ее постановку в
виде системы уравнений (создание математической модели), а не на конкретные методы
ее решения. Мы же не объясняем студентам, как вести арифметические вычисления
столбиком на бумаге или с помощью логарифмической линейки. В век калькуляторов
и компьютеров это делать не нужно и даже глупо.
Поясним этот тезис
конкретным примером –
расчетом термического КПД (ηt) идеальной газотурбинной
установки (ГТУ), работающей по термодинамическому циклу Брайтона [7] с двумя
изобарами и двумя изоэнтропами. Во всех справочниках,
учебниках и задачниках можно найти формулу для расчета этой величины:
|
|
(1) |
где π – это степень
повышения давления в компрессоре ГТУ (отношение давления за компрессором Р2 к давлению перед компрессором Р1), а
k – показатель адиабаты рабочего
тела цикла (отношение изобарной теплоемкости рабочего тела к его изохорной
теплоемкости). Во всех решебниках по термодинамике задача о термическом КПД ГТУ
решается простейшим способом: задаются значения k
и π и по формуле (1) рассчитывается требуемое
значение. При этом, как правило, не объясняется, как была
получена формула (1), что нужно сделать, чтобы учесть зависимость показателя
адиабаты k от температуры и давления рабочего
тела, состав которого по циклу меняется (воздух, смесь воздуха с топливом,
дымовые газы), как учесть «неидеальность» процессов
сжатия в компрессоре и расширения рабочего тела в газовой турбине и т.д.
На рис. 3 показан
иной, открытый подход к решению данной задачи.

Рис. 3. Открытый, интерактивный,
сетевой расчет КПД ГТУ
Исходными данными для
расчета КПД ГТУ (рис. 3) являются: давление рабочего тела на входе в компрессор
Р1, степень повышения давления в компрессоре π,
температура рабочего тела на входе в компрессор Т1 и на входе в газовую турбину
Т3, а также значения удельных изобарной (Cp) и
изохорной (Cv)
теплоемкостей рабочего тела («идеальный» воздух: Ср
= ![]() R и Сv =
R и Сv = ![]() R, где R – универсальная газовая постоянная).
R, где R – универсальная газовая постоянная).
Для определения
термического КПД ГТУ рассчитываются значения удельной энтальпии рабочего тела Н
во всех четырех точках цикла через взятие определенного интеграла по
температуре от значения Cp. Определенный интеграл
задействован и при определении значений удельной энтропии S во всех точках цикла. Тут сразу
можно возразить, что в расчете, показанном на рис. 3, интегралы можно убрать,
приняв во внимание, что переменная Cp является константой и может быть
выведена из-под интеграла. Но… в реальных ГТУ
задействовано реальное рабочее тело, у которого теплоемкость зависит от
температуры. Подход к решению задачи о КПД ГТУ, показанному на рис. 3,
позволяет учесть такую зависимость Cp = f(T). Кроме того, можно также учесть
другую «неидеальность» –
рост энтропии рабочего тела при его сжатии в компрессоре (не S2 = S1, а S2 > S1) и расширении в газовой турбине
(не S4
= S3,
а S4
> S3).
Несложно также учесть
и другие «реальности»: потери давления в камере сгорания (Р3 ≠ Р2) или в «атмосфере» (Р4 ≠ Р1). Формула
(1) является закрытой, ничего не дающей ни «душе» (сфера образования),
ни «телу» (промышленность). Расчет же, показанный на рис. 3, открыт
и для изучения (образование) и для его расширения, привязки к реальным схемам
ГТУ (промышленность).
Особо следует отметить расчеты в
точках 2 и 4 нашего термодинамического цикла. В этих точках расчет значений температуры
ведется не по готовым заранее введенным формулам, а в процессе решения
интегрального уравнения блоком Given
(дано) – Find
(найти) пакета Mathcad.
Это опять же существенно повышает уровень открытости задачи.
3) Технология MAS позволяет задачи решебников как бы «вывернуть на изнанку» – не считать по готовым формулам, меняя исходные данные, а самому обучаемому[5] вводить в расчет нужные формулы. И не только выбором формулы из предложенного списка[6], а непосредственным вводом нужной формулы в расчет. На рис. 4 показан пример такой работы – расчет термического КПД термодинамического цикла Отто.

Рис. 4. Сетевой, интерактивный экзамен по термодинамике
Опрашиваемый, открыв в Интернете страницу, показанную на рис. 4, должен ввести в текстовые окна уравнение, по которым рассчитываются те или иные термодинамические величины в точках 1, 2, 4 и 4 цикла Отто. Если уравнения составлены и введены правильно (а это и отображено на рис. 4 – сразу после открытия данной страницы Интернета текстовые окна были пустыми), то после нажатия клавиши Recalculate итоговый ответ, найденный по открытому алгоритму расчета термодинамического цикла (см. выше), должен совпадать с тем, какой получен по упрощенной («закрытой») формуле, также приведенной в расчете. В данном Интернет-тесте по термодинамике при расчете параметров цикла Отто в точках 2 и 4 приходится составлять и решать уже не одиночное интегральное уравнение (см. рис. 3 с расчетом ГТУ), а систему интегро-алгебраических уравнений: уравнение Клайперона–Менделеева и уравнение, правая часть которого – определенный интеграл, по которому высчитывается энтропия рабочего тела в данной точке и где верхний предел интеграла – это одно из двух неизвестных системы уравнений.
Авторы данной статьи со своими студентами взялся за
труд перевести некоторые задачники и решебники, связанные в первую очередь с
энергетикой, в сетевой, интерактивный, открытый формат. При такой «оцифровке»,
как уже отмечалось, выявляется множество ошибок и опечаток. И это не только
классические ошибки/опечатки (в степени переменной стоит двойка, а не
положенная тройка, например), а некие недомолвки/умолчания, в которых может, в
конце концов, разобраться специалист или даже студент, получающий
дополнительные качественные консультации у преподавателя. Но
математические пакеты такие недомолвки/умолчания категорически отказываются
«извинять», прерывают счет сообщениями об ошибке или выдают ответ, не
совпадающий с книжным… И в этом трудно винить авторов, редакторов, а тем более
корректоров таких задачников и решебников: одно дело вычитать «гладкий» текст,
а другое – тщательно проверить формулы, не прибегая к скрупулезному счету по
ним.
Вот неполный перечень справочников, учебников и
решебников, расчеты которых открыты на сайте www.vpu.ru/mas:
• по
высшей математике http://twt.mpei.ac.ru/math
• по
физическим величинам http://twt.mpei.ac.ru/pvhb
• по
теплотехнике и теплоэнергетике http://twt.mpei.ac.ru/tthb
• по
теплофизическим свойствам рабочих тел энергетики http://twt.mpei.ac.ru/ochkov/WSPHB/index.html
• по
термодинамическим циклам http://twt.mpei.ac.ru/TTHB/2/ThermCycleMCS.html
• по гидрогазодинамике http://twt.mpei.ac.ru/gdhb
• по
трубопроводам ТЭС http://twtmas.mpei.ac.ru/mas/Worksheets/HBPipePP
• по
химической кинетике http://twtmas.mpei.ac.ru/mas/Worksheets/Chem/ChimKin.html
• по
химической термодинамике http://twt.mpei.ac.ru/TTHB/1/HBThermValues.html
• по электробезопасности http://twt.mpei.ac.ru/TTHB/EB
• по тепломассообмену http://twt.mpei.ac.ru/ochkov/Diff_MC/web_HMT/index_HMT_E-Book.htm
• по
ионообменным смолам http://twt.mpei.ac.ru/TTHB/1/Dow
• по
теории автоматического регулирования http://twtmas.mpei.ac.ru/mas/Worksheets/Rotach
• по
снижению шума от энергетического оборудования http://twt.mpei.ac.ru/TTHB/1/Tupov.html
и
др.
К особому типу решебников можно отнести сборники различного
рода нормативных документов (строительные нормы и правила – СНиПы, например), где также много формул и которые также
можно и нужно «оживить» в Интернете. Что, кстати, уже делается, в том числе и одним
из авторов данной статьи в отношении некоторых стандартов энергетики. Так на
сайте http://twt.mpei.ac.ru/MCS/Worksheets/Thermal/Izol-Trub-Teploset.xmcd
читатель
может увидеть пример одного из таких «живых» нормативных документов – СНиП по расчету толщины теплоизоляции теплосети.
Недостаточная толщина изоляции приводит к недопустимым тепловым потерям, а
избыточная – к перерасходу теплоизоляционного материала. Эту типичную
технико-экономическую задачу (минимизация общей стоимости проектирования,
сооружения, эксплуатации и последующей утилизации промышленного объекта при
полном выполнении им своих функций) можно каждый раз решать индивидуально, а
можно воспользоваться обобщенными СНиПам,
что в конечном итоге ведет к удешевлению проектирования.
Одним из способов оценки эффективности работы и определения нормативных расходов условного топлива в широком диапазоне режимов, а также диагностики паровых турбин является сравнение их параметров с типовыми энергетическими характеристиками турбоагрегатов (ТЭХ), выпущенных в «бумажных» вариантах в 1970-90 гг. Фирма ОРГРЭС (www.orgres-f.ru) совместно с МЭИ (www.mpei.ru
) провела работа по
переработке с использованием современных информационных технологий и публикации («выкладыванию») характеристик турбин в
интернете – см. http://twtmas.mpei.ac.ru/mas/Worksheets/Turbine/index.html.
Ведя разговор о нормативных документах, нельзя не
коснуться проблемы сертификации расчетов. Страницы Интернета, как правило,
отданы на откуп случайным создателям и не подвергаются жесткому редактированию
и тщательной корректуре в то время как достоверность
информации в «бумажных» справочниках в какой-то мере подтверждается солидностью
соответствующих издательств с их штатом научных консультантов, редакторов и
корректоров. С другой стороны, авторы собрали довольно
большую коллекцию опечаток в справочниках весьма солидных издательств, когда
вместо, например, 0,02387 стоит 0,02387 (двойка перестала быть
нижним индексом, отмечающим повторяющиеся нули), а вместо 27,39 – 72,93
(вероятно, число набрал человек, знающий немецкий язык, на котором говорят не
«семьдесят два», а «два и семьдесят», не «девяносто три», а «три и девяносто»)
и т.п. Такие ошибки практически невозможно выявить при традиционной
(визуальной) правке корректур «бумажных» справочников и мы уже это отмечали.
Тем не менее, ошибки остаются ошибками со всеми вытекающими последствиями.
Сертификацию расчетных документов, опубликованных в
Сети, можно проводить двумя способами. Во-первых, можно публиковать в Сети
письмо «солидной» организации, где подтверждается правильность расчетов.
Во-вторых, можно из сайтов «солидных» организаций делать ссылки на
соответствующие расчетные сайты и упоминать об этом на самом расчетном сайте.
«Оживление» расчетов, приводимых в справочниках,
учебниках и монографиях, проводит, например, американская фирма Knovel, с
которой авторы активно сотрудничают. На сайте фирмы www.knovel.com
(рис. 5) опубликованы книги по различным областям науки и техники в
pdf-формате –
см. символ ![]() на рис. 5. В настоящее время ведется
работа по дополнению электронных текстов книг, где приводятся «мертвые»
расчеты, файлами, которые можно запустить в среде Mathcad и сделать расчет с
новыми исходными данными
на рис. 5. В настоящее время ведется
работа по дополнению электронных текстов книг, где приводятся «мертвые»
расчеты, файлами, которые можно запустить в среде Mathcad и сделать расчет с
новыми исходными данными ![]() .
.

Рис. 5.
Сайт фирмы Knovel
Кстати, при общении со специалистами фирмы Knovel
прозвучал упрек в том плане, что абонентами сайта www.knovel.com
(англоязычный, естественно, ресурс) является весь мир, включая страны Восточной
Европы – Чехия, Словакия, Венгрия и т.д. Но только пользователей из России
в списке абонентов сайта почти нет. На этот упрек один из авторов ответил так. Чехия, Словакия, Венгрия и другие страны раньше пользовались
немецкими книжными ресурсами, затем перешли на русские (советские) ресурсы,
сейчас используют английские, в том числе и электронные ресурсы, а в будущем,
вполне вероятно, перейдут на китайские ресурсы… Россия же, включая,
естественно, советский период, всегда имела собственную высокую
научно-техническую культуру – русскоязычные справочники, учебники,
монографии (включая, и переводные) почти по всем отраслям знаний. Это с
одной стороны, хорошо (хорошо иметь собственную культуру, включая техническую),
а с другой, плохо, т.к. это приводит к некой самоизоляции, которая часто
приводит к снижению качества тех или иных справочников, учебников, монографий.
Выводы:
«Оживление», учебников,
задачников и решебников в Интернете позволяет:
провести
ревизию правильности постановки и решения задач в «бумажных» учебниках и
задачниках
открыть в
Интернете задачи практической направленности
организовать
контроль знаний посредством решения задач не через вычисления, а
непосредственно через ввод формул.
Литература[7]:
1. Очков В.Ф. Mathcad и некоторые тайны художественной литературы // Домашний компьютер, № 5, 2000
2. Очков В.Ф. Физические и экономические величины в Mathcad и Maple. М.: Финансы и статистика, 2002
3. Очков В.Ф., Яньков Г.Г. Комплекс "справочник+сайт интернета" и проблема передачи знаний // Труды Академэнерго, № 1, 2009
4. Очков В.Ф. MA и MAS: проблемы и решения при создании web-ресурсов сферы образования. Вопросы Интернет Образования, № 29, 2005
5. Очков В.Ф. Mathcad 14 для студентов и инженеров: русская версия. BHV-Петербург, 2009
6. Брюханов
О.Н., Коробко В.И., Мелик-Аракелян
А.Т. Основы гидравлики, теплотехники и аэродинамики: Учебник. – М.:
ИНФРА-М, 2008
7. Александров А.А., Орлов К.А., Очков В.Ф. Математические пакеты – новые подходы при расчетах
процессов термодинамики и других научных дисциплин. // Известия высших учебных
заведений. Проблемы энергетики. №11-12, 2005
Послесловие к эпиграфу
Да, в отечественной «гоголиане» нет разъяснений и даже упоминаний, касающихся вычислительной ошибки эпиграфа. Вернее, автор не нашел в Интернете, вернее, в Рунете каких-то разъяснений по этому поводу, хотя самих комментариев к «Мертвым душам» во Всемирной паутине море. Но тут возникла необходимость перевести статью на английский язык. Естественно, эпиграф статьи переводить не стали, а стали искать уже готовый его перевод на английский. Переводчики, как известно, народ дотошный – они сразу увидели ошибку в данном отрывке из поэмы Гоголя. Естественно, ее не исправили («Из песни слова не выкинешь!»), но обвесили комментариями в том плане, что Гоголь не просто обсчитался, а сделал это намеренно – то ли Чичиков просто хотел обмануть Плюшкина при расчете за мертвые души, то ли Чичиков просто оговорился «по Фрейду», невольно показав в этой ошибке всю свою мелочную душу и т.д. т.п.
Отсюда такая неожиданная аналогия.
При переводе художественной литературы на иностранный язык выявляются многие ошибки и неточности оригинального текста.
При «оживлении» формул научно-технической литературы, о котором рассказано в статье, при переводе этих формул на язык современных информационных технологий также «всплывают» ошибки.
С другой стороны, стоит отметить, что переводчики очень часто в тексты вносят свои ошибки, связанные, например, с неполным совпадением исходного слова с его переводом: в словарях, как правило, одному слову из одного языка соответствует множество слов из другого языка.
При оживлении формул «сторонним переводчиком» они могут также быть несколько искажены. Поэтому вывод – таким «оживлением» должен заниматься сам создатель формул, а не сторонний переводчик. Набоков, как известно, сначала сам стал переводить на английский свои русские тексты, а потом стал просто сразу писать по-английски. В этом, наверно, кроется одна из причин популярности Набокова и у нас и на Западе.