Необычные математические часы
или
Обратная задача
коммивояжера
Богомолова Е.П., Очков В.Ф.
Национальный исследовательский университет «Московский энергетический институт»
Аннотация
В статье рассмотрены некоторые математические задачи, приложенные к часам. Показано, как можно использовать часы на занятиях по математике для иллюстрации некоторых математических задач
Ключевые слова:
Часы, простые числа, задача коммивояжера, Mathcad, Первое апреля
Современные обычные часы – это круглый диск со стрелками. По периметру такого диска расположены двенадцать арабских или римских цифр, образуя циферблат. Но нет на свете человека, которого бы оставили равнодушными необычные часы, как по форме, так и по содержанию. С момента изобретения часов люди не переставали менять не только их, устройство (солнечные, песочные, водяные, механические, электронные, атомные и т.д.), но и их внешний вид, преследуя при этом и практические, и декоративные цели. Если говорить о практических целях, то тут можно вспомнить нестандартные часы с 24-х часовым циферблатом. Такие часы (хронометры) размещают на кораблях (морских, воздушных, космических), чтобы не спутать день с ночью. Есть часы с двумя циферблатами, показывающими путешественнику и местное и «родное» время. В гостиницах и офисах можно увидеть часы с несколькими циферблатами, вернее, несколько связанных часов, фиксирующих время в ключевых столицах мира: Tokyo, Moscow, Paris, London, New York и т.д.
Смешанные практические и декоративные функции несут так называемые цифровые часы, где время отмечается не стрелками («аналоговые» часы»), а числами: 14:21:37, например. Такие часы когда-то были и механическими, а сейчас они, как правило, только электронные. Наиболее практичными считаются часы, где время отмечается стрелками (по стрелкам проще оценивать, сколько времени осталось до какого-то события), а календарная дата – числами.
Но основные «изыски и изощрения» в сфере необычности часов развернулись на чисто «декоративном фронте». В этом можно убедиться, если в Интернете сделать запрос по ключу «Необычные часы». Каких только часов там не увидишь?! Вершина дизайнерского аскетизма – вращающиеся у стенки две стрелки разной длины без каких-либо цифр или других меток на циферблате, которого, кстати говоря, у таких часов совсем и нет. Другая крайность – перегруженность часов различными «художественными излишествами». Глядя на некоторые подобные часы, долго ломаешь голову, чтобы понять, какое время они показывают. Часто в этой «головоломке» и заключена вся дизайнерская суть таких «часов», доходящая иногда до абсурда. Читаем у Даниила Хармса – мастера литературного абсурда: «На дворе стоит старуха и держит в руках стенные часы. Я прохожу мимо старухи, останавливаюсь и спрашиваю ее: «Который час?» – Посмотрите, – говорит мне старуха. Я смотрю и вижу, что на часах нет стрелок. – Тут нет стрелок, – говорю я. Старуха смотрит на циферблат и говорит мне: – Сейчас без четверти три» [1].
Из всех часов необычной формы особо выделяются часы с неким математическим смыслом. Безусловно, математика присутствует во всех часах – стоит только вспомнить о дифференциальном уравнении колебания маятника, балансира или кремневого кристалла, на которых основан ход современных часов [2]. В некоторых часах корпус делают прозрачным, чтобы была видна вся их внутренняя «механико-математическая сущность». Но мы сейчас поговорим о внешней, так сказать, математике часов.
Есть часы не с цифрами 1, 2, 3…12, а с математическими выражениями
на циферблате. В этой «декоративности» можно отметить и
некую «практичность» – такие часы будут уместны, например, в школьном кабинете
математики: ученики, поглядывая на часы, будут запоминать таблицу квадратов
натуральных чисел. На рис. 2 показаны часы, где вместо цифр записаны
математические формулы и выражения, по которым эти цифры можно вычислить в
среде инженерного калькулятора Mathcad. Читатель по этим часам может не только
узнать текущее время, но и оценить свои знания математики и пакета Mathcad –
все ли формулы и обозначения чисел ему понятны [3]!?
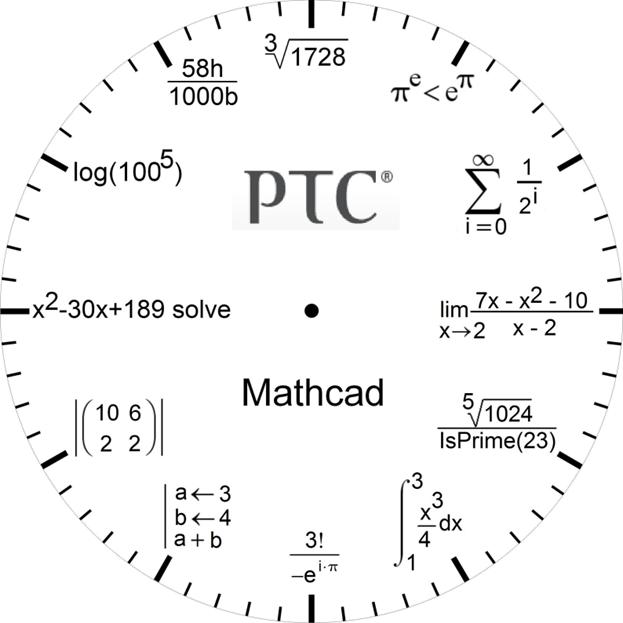
Рис. 1. Часы с «математическим»
циферблатом
Легко заметить, что вместо привычных натуральных чисел 1, 2, …,12, записанных цифрами от 0 до 9, на циферблат можно поместить те же самые числа, но записанные только с помощью цифр 1, 2 и 3, операций сложения, умножения и возведения в степень. Действительно: 4=22; 5=21+31; 6=21·31; 7=22+31; 8=23; 9=32; 10=23+21; 11=23+31; 12=22·31.
Стоит напомнить, что 2 является единственным четным простым числом, а 3 – первым нечетным простым числом. Единица не считается простым числом, хотя и является ключевым в возникновении этого понятия. Евклид определял простые числа так: «Простое число есть измеряемое только единицей». О каких же измерениях здесь идет речь? О самых привычных измерениях отрезка числовой оси от нуля до натурального числа посредством многократного откладывания отрезка единичной длины. Все натуральные числа, большие единицы, и не являющиеся простыми, можно помимо единицы «измерить», по крайней мере, еще одним числом. Т.е. можно откладывать отрезок, например, длины 2 (четные числа), или 5 (числа, кратные пяти). Такие числа называются составными. Говоря строго математически, простые числа не имеют других делителей, кроме единицы и самого себя. Саму единицу математики предпочитают не считать простым числом, еще и потому, что в этом случае многие важные теоремы теории чисел формулируются проще.
В обозначении часов на циферблате, что удивительно, участвуют ровно 6 (половина от 12) составных чисел: 4, 6, 8, 9, 10 и 12; 5 простых чисел и единица. Таким образом, простые числа составляют почти 42% чисел первой дюжины. Всегда ли они расположены так часто?
Для того чтобы это понять, математики ввели функцию 
– количество простых
чисел, не превосходящих 
, и специальную величину 
, называемую средней плотностью простых чисел среди первых натуральных чисел.
Изучение таблиц простых чисел показывает, что с ростом простые числа
встречаются в среднем всё реже и реже (хотя все же чаще квадратов натуральных
чисел). Эйлер доказал, что 
, т.е. чем длиннее отрезок 
, тем меньший процент от всех натуральных чисел на этом
отрезке составляют простые числа. Но если предел плотности равен нулю, то,
возможно, что рано или поздно все простые числа «закончатся»? Оказывается, что
это невозможно. Теорему о бесконечном множестве простых чисел мы легко докажем
с вами прямо сейчас.
Предположим, что нашлось самое большое (и поэтому последнее) простое число. Перемножим все известные простые числа, включая наибольшее, а к произведению добавим единицу. Если полученное таким способом число делить на каждое из известных простых чисел, то в остатке мы получим 1, т.е. новое число не делится ни на одно простое число. Поэтому оно не делится ни на одно составное число, т.к. каждое составное число, в свою очередь, является произведением некоторых простых чисел. Итак, мы нашли число, которое больше любого известного простого числа и делится только на 1 и на себя, т.е. само является простым, превосходящим все известные простые числа. Мы получили противоречие, а это означает, что наибольшего простого числа не существует.
Если вам захочется узнать, какие же простые числа лежат между двумя заданными натуральными числами, то вы сможете отыскать их, используя Mathcad-функцию IsPrime (см. «четыре часа» на рис. 1), определяющую, являются ли аргумент простым числом, и/или оператор factor, раскладывающий составное число на простые множители – см. рис. 2. Кстати, разложение большого числа на простые множители – это довольно сложная и длительная математическая операция. Одни из самых распространенных алгоритмов шифрования текстов основан на разложении числа на простые множители.
Рис. 2. Анализ числа «на простоту» в
среде Mathcad
Из рис. 2 видно, что 1 – не является ни простым числом, но, тем более, составным. Показаны также два первых простых числа с двумя и девятнадцатью цифрами-единицами. Следующие такие простые числа составлены из 23, 317, 1031 и т.д. единиц. Кстати, поиск таких «одноединичных» простых чисел («и т.д.») – это отдельная интересная задача.
В оформление часов иногда закладывают сложные математические алгоритмы. Одна корейская фирма выпускает часы (рис. 3) в виде решения задачи коммивояжера. Несколько слов о самой задаче. Вот что о ней можно прочесть в Википедии (www.wikipedia.org): «Задача коммивояжера (разъездного торговца) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании наивыгоднейшего маршрута, проходящего через указанные города с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешевый и т.п.) и соответствующие данные о расстояниях, стоимости и т.п.». Коммивояжер при этом должен побывать в каждом городе только один раз. Задача коммивояжера имеет много практических приложений. Прежде всего, это оптимизация маршрутов – оптимальная логистика, как принято сейчас говорить. Читаем в романе Л.Н. Толстого «Воскресенье»: «Сообразив, куда прежде, куда после ехать, чтобы не возвращаться, Нехлюдов прежде всего направился в сенат» [4]. Классические коммивояжеры (коробейники, офени) сейчас практически перевелись, хотя на дверях многих офисов до сих пор можно увидеть табличку типа «Торговым агентам вход запрещен!» Задачу коммивояжера решает курьер, отправляющийся развозить заказы клиентов сетевого магазина, торгующего электроникой, лекарствами, книгами и прочим. Есть и не вполне обычные приложения задачи коммивояжера. Так, например, расшифровать геном живого организма невозможно без решения довольно сложной задачи коммивояжера.
Рис. 3. Часы-глобус
с задачей коммивояжера
На глобусе часов с задачей коммивояжера (рис. 3) каждые сутки ровно в полночь световыми точками отмечаются 1440 населенных пунктов нашей планеты, выбранные случайным образом из почти двух миллионов, хранящихся в памяти часов (см. ниже рис. 8). Внутри глобуса установлен миниатюрный планетарий, высвечивающий эти точки на поверхности глобуса. Число 1440 – это количество минут в сутках. Более крупными световыми точками на глобусе выделяются 24 узловых населенных пункта («города»). Это будут часы в сутках. Далее выбирается первый случайный город, в который помещается «коммивояжер» и которому дается задание обойти все населенные пункты, руководствуясь алгоритмом ближайшего соседа – из очередного города коммивояжер идет в ближайший город, который он еще не посетил. На цифровой панели этих часов высвечиваются две цифры: номер города, из которого вышел наш коммивояжер (0, 1… 23 – часы) и номер населенного пункта, который он только что прошел (0, 1… 59 – минуты). Пройденный маршрут на глобусе высвечивается линиями, соединяющими отдельные точки. Человек, смотрящий на такие часы, может не только узнать, какое сейчас время, но и увидеть, где сейчас находится коммивояжер, и оценить, куда он пойдет в следующую минуту. На панели часов помимо текущего времени высвечивается название пройденного населенного пункта, а из динамиков звучат типичные мелодии и песни данного региона Земли. Динамики часов могут, конечно, выполнять и свою основную функцию – транслировать радиопередачи. Глобус часов можно также использовать по прямому назначению – для изучения политической карты мира.
Другие подобные, но уже не настольные, а настенные часы висят на вокзале швейцарского города Люцерн. Швейцария – это страна часов и путешественников и такие часы там очень уместны. На этих часах (плоская плазменная панель) прорисован контур Швейцарии. Каждые сутки в полночь на этой карте высвечивается 1440 случайных городов, деревень и отдельно стоящих отелей этой альпийской страны. Человек, приехавший на вокзал в города Люцерн, может не только уточнить время по таким часам, но и при желании будет следить за передвижением «коммивояжера», угадывать, куда он повернет в следующую минуту. Это скрасит ожидание поезда, заставит задуматься о задаче коммивояжера, об оптимизации собственного путешествия по Швейцарии, Европе, миру…
На рис. 4 и 5 показано упрощенное графическое отображение «циферблата» таких часов. В прямоугольной области случайным образом размещаются 1440 квадратиков, 24 из которых накрываются кружечками, которые нумеруются числами от 0 до 23. В полночь из нулевого города (см. верхний левый угол на рис. 4 и 5) выходит «коммивояжер» и за 24 часа посещает все города. На рис. 4 показан «полдень» нашего путешественника (12:00:00), а на рис. 5 – минута до полуночи.
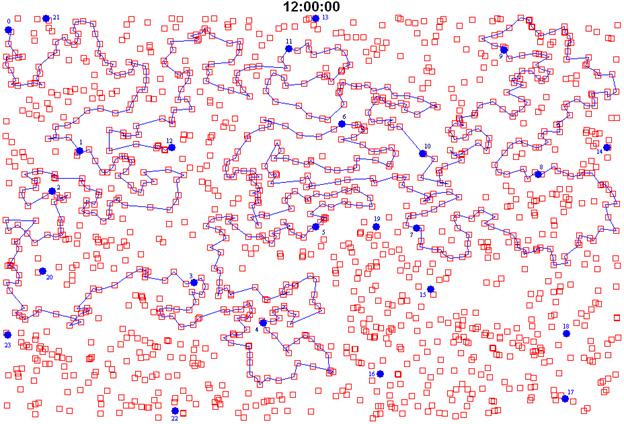
Рис. 4. Часы с задачей коммивояжера –
полдень
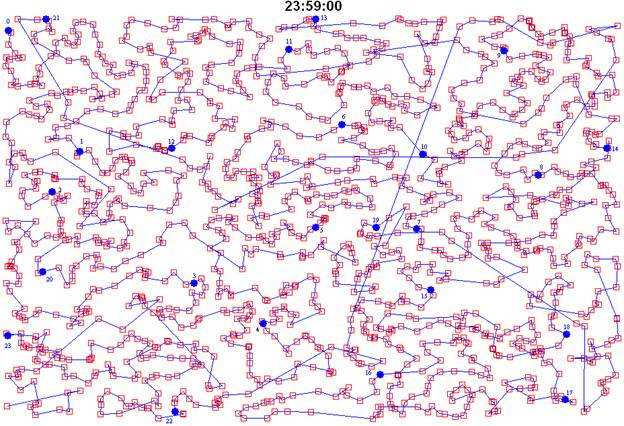
Рис. 5. Часы с задачей коммивояжера – без
одной минуты полночь
В задачу коммивояжера, отображенную на рис. 4 и 5, заложен уже упоминавшийся алгоритм ближайшего соседа: из очередного города коммивояжер идет ближайший город, который он еще не посещал. Алгоритм ближайшего соседа относится к разряду «жадных» алгоритмов. Из-за этой «жадности» нашему коммивояжеру приходится петлять, а в конце своего турне перескакивать в отдаленные города (см. рис. 5), ранее опрометчиво пропущенные. Все это увеличивает общую длину маршрута.
Посетители вокзала города Люцерн, глядя на такие необычные часы, могут задумываться не только «о времени и пространстве», но и еще кое о чем…
Швейцария – страна не только часов и путешественников, но и банкиров, одно из качеств которых – это профессиональная «жадность», выражающаяся, в частности, в том, что банкиры стараются брать деньги у клиентов на хранение в банке под минимальные проценты, а давать кредиты под максимальную ставку. Профессиональная жадность заставляет банкиров раздавать кредиты даже тем, кто деньги может и не вернуть. Это одна из причин финансового кризиса, охватившего недавно почти весь мир, погубившего многие банки, и поставившего некоторые страны на грань финансового краха[1]. Коммивояжер, пропуская нужный город и «жадно» направляясь к ближайшему, увеличивает свой маршрут. Банкир, гоняясь за сиюминутной прибылью, снижает общую прибыль банка.
Алгоритм ближайшего соседа подкупает простотой своей реализации: задачу можно решить с помощью циркуля, карандаша и линейки. После того, как все города будут соединены линиями, можно попытаться распутать некоторые петли, сократив тем самым общую длину маршрута. Но математики разработали более оптимальные алгоритмы решения задачи коммивояжера. Один из них подсказала живая природа. Люди заметили, что муравьи, найдя новый источник питания, сначала таскают пищу из него в свой муравейник случайными разбросанными маршрутами. Но постепенно разброс маршрутов стягивается в один единственный – кратчайший. Вот как об этом написано в той же Википедии: «В реальном мире муравьи первоначально ходят в случайном порядке и по нахождению продовольствия возвращаются в свою колонию, прокладывая феромонами[2] тропы. Если другие муравьи находят такие тропы, они, вероятнее всего, пойдут по ним. Вместо того, чтобы отслеживать цепочку, они укрепляют её при возвращении, если в конечном итоге находят источник питания. Со временем феромонная тропа начинает испаряться, тем самым уменьшая свою привлекательную силу. Чем больше времени требуется для прохождения пути до цели и обратно, тем сильнее испарится феромонная тропа. На коротком пути, для сравнения, прохождение будет более быстрым и как следствие, плотность феромонов остаётся высокой. Испарение феромонов так же имеет свойство избежания, стремления к локально-оптимальному решению. Если бы феромоны не испарялись, то путь, выбранный первым, был бы самым привлекательным. В этом случае, исследования пространственных решений были бы ограниченными. Таким образом, когда один муравей находит (например, короткий) путь от колонии до источника пищи, другие муравьи, скорее всего, пойдут по этому пути, и положительные отзывы в конечном итоге приводят всех муравьёв к одному, кратчайшему, пути».
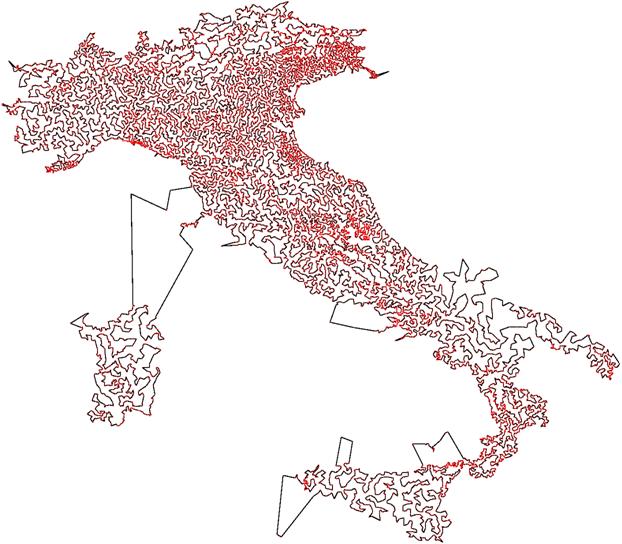
Рис. 6. Путь коммивояжера по Италии
Рис. 7. Задача коммивояжера и Мона
Лиза
Рис. 8. Мировое турне коммивояжера
На рис. 6 показан путь коммивояжера, проложенный с помощью муравьиного алгоритма по 16 862 населенным пунктам Италии [5]. Естественно, путешественник, пожелавший обойти самым коротким путем все «города и веси» какой-либо страны, далеко не всегда сможет по прямой линии перейти из одного населенного пункта в другой. Ему часто придется идти обходными путями по существующим дорогам и тропам. Недавно в Google появился специальный сервис, позволяющий оптимизировать маршруты передвижения не только из пункта А в пункт В, указанные на карте мира, но и по круговым маршрутам (турам), используя при этом автомобиль, поезд, самолет и другие средства передвижения.
Решение задачи коммивояжера, как и в случае с оформлением часов может совсем уходить от практики в сторону чистой декоративности. Есть направление в живописи под названием пуантилизм, когда художник пишет картину точечными мазками. На рис. 7 показан вариант знаменитой картины Леонардо да Винчи, где Мона Лиза прорисована 100 000 точками, соединенными «тропой коммивояжера». Чисто декоративным можно также считать и путь коммивояжера через 1 904 711 населенных пунктов Земли – см. рис. 8.
Но вернемся к вокзальным часам в швейцарском городе Люцерн.
Путешественник в отличие от коммивояжера часто намерено выбирает не наикратчайший маршрут, а маршрут, отвечающий каким-то другим критериям. Маршрут может быть даже и наидлиннейшим. В связи с этим можно говорить об обратной задаче коммивояжера, о задаче нахождения самого длинного пути.
На рис. 9 показан путь коммивояжера через 979 городов и деревень Люксембурга при использовании жадного алгоритма для отыскания наикратчайшего маршрута.
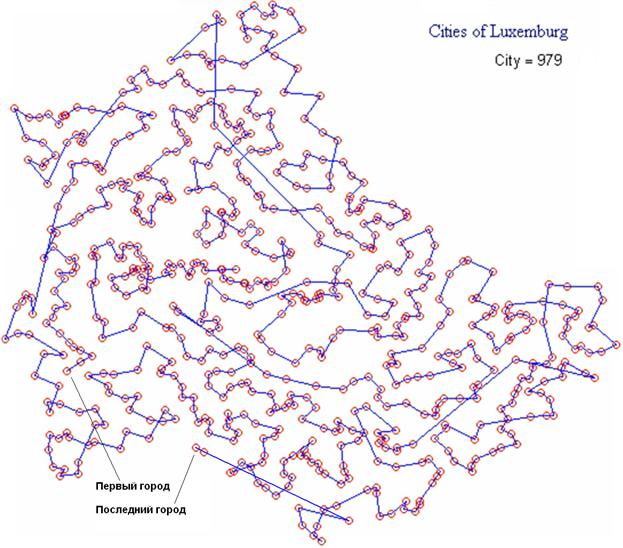
Рис. 9. Путь коммивояжера при
использовании жадного алгоритма для отыскания наикратчайшего маршрута
Из рис. 9 (как, впрочем, и из рис. 4 и 5) видно, что выбранный маршрут не самый оптимальный, т.к. коммивояжеру, повторяем, из-за своей «жадности» приходится делать петли. Кроме того, можно показать, что длина «жадного» маршрута сильно зависит от выбранного первого города. На рис. 9 этот первый город отмечен. Он является оптимальным в том смысле, что были перебраны все города в качестве стартового и зафиксирован тот, путь из которого по жадному алгоритму оказался минимальным. Еще один признак неоптимальности пути коммивояжера, показанного на рис. 9, состоит в том, что длины первой и последней половины пути сильно отличаются. На рис. 10 показана Mathcad-программа [6] отыскания пути коммивояжера (вектор way) методом ближайшего соседа.
Рис. 10. Mathcad-программа
метода ближайшего соседа
Исходными данными для программы являются вектора X и Y, хранящие декартовые координаты городов. Расчет начинается с формирования квадратной матрицы М, хранящей расстояния между городами и бесконечность (∞) на главной диагонали. Значения бесконечности будет присваиваться элементам матрицы Mi,j и Mj, i, если коммивояжер уже прошел путь от i-го до j-го города или наоборот. «Гвоздем» программы являются функции min и match. Функция min возвращает минимальный элемент своего аргумента-вектора, а функции match – место этого элемента в векторе.
Но если в программе функцию min заменить на функцию max, то она будет возвращать… максимальный путь коммивояжера, когда он из очередного города направляется не в ближайший, а самый дальний. Этот маршрут, вернее, его последний участок показан на рис. 11.
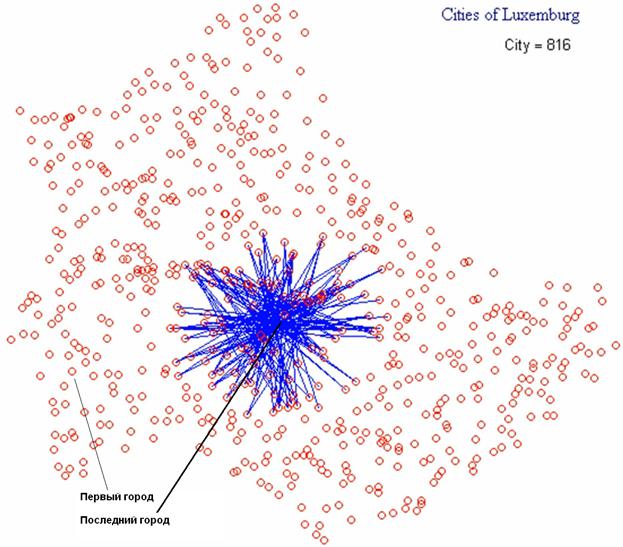
Рис. 11. Завершение пути коммивояжера по «щедрому»
алгоритму
Назовем этот алгоритм «щедрым» и также отметим, что его длина зависит от выбранного начального города. На рис. 11 этот город тот же, какой был выбран при реализации «жадного» алгоритма (рис. 9), но можно опять же перебором выбрать город, путь коммивояжера из которого по «щедрому» алгоритму окажется самым длинным. Эту задачу мы поручаем читателю, отсылая его за нужными программами и другими данными на сайт статьи – http://twt.mpei.ac.ru/ochkov/SalesMan. Еще более длинный маршрут можно получить, если, например, применить вышеописанный «муравьиный» алгоритм к матрице, хранящей обратные расстояния между городами.
Литература и Интернет-источники:
1. Даниил Хармс «Старуха» – http://lib.ru/HARMS/staruha.txt
2. Очков В.Ф. «MCS на занятиях по математике, физике, информатике…» // Компьютерные учебные программы и инновации. № 3. 2008 – http://twt.mpei.ac.ru/ochkov/Pendulum
3. Сайт http://communities.ptc.com/thread/32536
4. http://az.lib.ru/t/tolstoj_lew_nikolaewich/text_0090.shtml
5. Сайт http://www.tsp.gatech.edu
6. Очков В.Ф. Mathcad 14 для студентов и инженеров: русская версия // БХВ-Петербург, 2009 г. – http://twt.mpei.ac.ru/ochkov/Mathcad_14/RusIndex.html