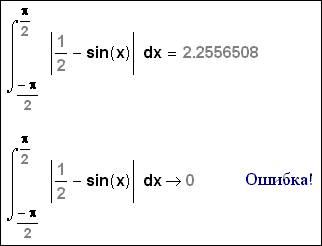Эта статья – побочный продукт работы автора над двумя книгами серии «Mathcad для профессионалов[1]»: «Советы пользователям Mathcad» и «Физические величины в Mathcad». В разгар работы над книгами (конец 2000 г.) появилась новая версия Mathcad – Mathcad 2001. Но не конечный (коммерческий) продукт, а бета-версия[2]. Это потребовало внести коррективы в вышеотмеченные книги. Предварительно автору пришлось изучить новинки Mathcad 2001, что и влилось в данную статью. Затем (февраль 2001 г.) автор получил полную версию Mathcad 2001 Premium и статью подправил.

Итак, что нового?!

1. Панели инструментов и меню

Знакомство с Mathcad 2001 начинается, естественно, с меню и с панелей кнопок-дублеров наиболее популярных команд меню, которые появляются на экране дисплея после запуска пакета, после входа в среду Mathcad 2001 – см. рис. 1:

Рис. 1. Панель инструментов Mathcad 2001

Тут всего одна новинка – одно изменение: справа от кнопки создания нового Mathcad-документа появилась кнопка, выводящая список шаблонов. Раньше (Mathcad 7, 8 и 2000) этот список можно было вывести на экран только через команду New… из меню File.

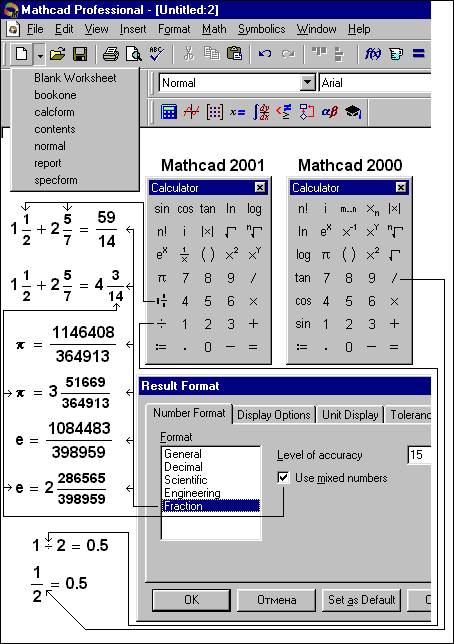
Что касается панелей инструментов, то изменения коснулись только панели Calculator: на рис. 1 эта панель выведена в «двух редакциях» – в редакции Mathcad 2000 и в редакции Mathcad 2001.

Что можно отметить нового в панели Calculator:

· Появилась кнопка ввода в расчет смешанной дроби. Теперь в среде Mathcad можно работать не только с десятичными, но и с простыми дробями и не только с невидимым символом умножения (2 а или 2а), но и с невидимым символом сложения: между целой и дробной частями выражения, вводимого в расчет новым оператором, стоит невидимый знак сложения (см. также статью автора «Невидимая переменная» – http://twt.mpei.ac.ru/ochkov/Invisible/Index.htm). В паре с новым оператором смешанной дроби работает новая опция форматирования численного ответа – см. диалоговое окно «Result Format» на рис. 1: теперь дробный ответ можно вывести не только в виде десятичной дроби с плавающей точкой, но и в виде простой дроби (Fraction), выделяя или не выделяя при этом дробную часть (см. галочку у подписи Use mixed number – использовать смешенное число). В виде простой дроби можно вывести значение двух основных математических констант: числа π и е (основание натурального логарифма) – см. рис. 1. Но эта возможность довольно спорная: здесь лучше бы получать не ответ в виде простой или смешанной дроби, а сообщение об ошибке. А то у пользователя может сложиться впечатление, что разработчики Mathcad решили проблему, над которой бились лучшие умы человечества в течение нескольких тысячелетий – представление числа π в виде простой дроби (проблема подобная проблеме квадратуры круга). Десятичная дробь у нас, как правило, ассоциируется с ограниченной точностью, а простая – с абсолютной (сравните 0.333… и 1/3). На рис. 1 числа π и е выведены в виде дроби, числители и знаменатели которых целые числа: тем не менее ответ ограничен в точности 15 знакам в мантиссе. Если это число уменьшать (см. поле с этим числом в диалоговом окне на рис. 1), то и выведенные численные значения констант π и е будут меняться соответствующим образом.

· Альтернативный оператор деления ¸, позволяющий вести это арифметическое действие в одну строку, появилось еще в Mathcad 2000. В среде Mathcad 2001 этот оператор можно вводить не только через аккорд [Ctrl+/], но и через соответствующую кнопку на панели Calculator. К двум встроенным операторам деления («двух- и одноэтажное деление») при необходимости можно добавить и два пользовательских. На рис. 1а показано, как это можно сделать:

Рис. 1a. Пользовательские операторы деления

Символы «/» и «:» можно ввести в расчет в виде символов операторов деления, заглушив аккордом [Shift+Alt+k] работу одноименных клавиш как макросов ввода оператора деления и оператора присваивания. После этого курсор поменяет свой цвет с синего на красный, что будет являться признаком «текстового» режима ввода спецсимволов[3]. Повторное нажатие (взятие) этого аккорда возвращает синий цвет курсору.

· На панели Calculator появилась кнопка 1/x. Она, как и кнопка ¸, не вводит в Mathcad новый оператор, а просто дублирует, ускоряет ввод в расчет старого оператора[4], возвращающего обратное значение операнда.

· На панели Calculator Mathcad 2001 после ввода трех новых кнопок остались те же 25 кнопок: с панели убрали кнопки m…n (переменная области, «недовектор»), X_n (n-й элемент вектора) и X^-1 (обратная матрица или скаляр). Теперь эти кнопки остались только на панели работы с матрицами.

2. Новая машинная арифметика

Эта ключевая новинка Mathcad никак не отображена внешне в меню или на панелях инструментов (см. рис. 1), но она может очень существенно повлиять на работу в среде Mathcad. Дело в том, что Mathcad – это программная среда интерпретирующего, а не компилирующего класса[5]. Из-за этого счет даже по не очень объемным документам (по отдельным «продвинутым» функциям – odesolve, например, решение краевой задачи в области дифференциальных уравнений) может длиться довольно долго. В среде Mathcad 2001 по умолчанию счет «форсирован» – см. радиокнопку во фейме Performance Preference диалогового окна Math Options, вызываемого командой Options… в меню Math (рис. 2):

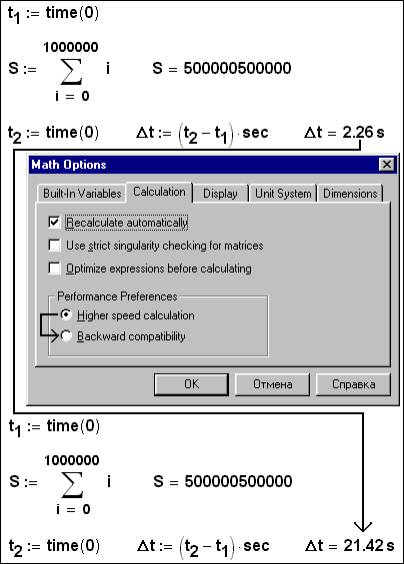
Рис. 2. Новые возможности вычислений в среде Mathcad 2001

На рис. 2 проведено сравнение обычной и ускоренной («форсированной») арифметики Mathcad на простейшей задаче – суммирование чисел натурального ряда в диапазоне от одного до миллиона. Ответы обычной и ускоренной арифметики (higher speed calculation), как и следует ожидать, получились одинаковыми (500000500000), но разница во времени счета оказалась существенной: ускоренная арифметика Mathcad работает почти на порядок быстрее (2.26 против 21.42 секунд). В испытаниях, отображенных на рис. 2 задействована недокументированная Mathcad-функция, возвращающая время работы системы в секундах. Само по себе это время нас не интересует[6], но разница времен (Dt) может существенно помочь провести скоростные испытания программ.

На рис. 2а можно видеть еще одну (старую) возможность ускорения счета. Это «оптимизация выражения перед вычислением – Optimize expression before calculating»: в этом случае счет предваряется анализом и упрощением выражения средствами символьной математики Mathcad, вернее, Maple. В нашем случае упрощение суммы дает выражение, счет по которому длиться доли секунды – см. рис. 2а:

Рис. 2a. Оптимизация счета через символьное преобразование

Правее оптимизированной формулы появляется красная шестиугольная звездочка. В России говорят, что это намек на то, что самые лучшие математики – это советские евреи (шутка: Что такое американский университет? Это место, где бывшие советские евреи преподают математику китайцам).

Но далеко не все задачи можно решить средствами символьной математики. Более того, аналитический ответ все равно приходиться дорабатывать численными методами (вычисление по формулам, построение графиков, поиск корней уравнений и т.д. и т.п.). Здесь же «форсированная» арифметика Mathcad очень пригодиться. Пригодиться также и такой совет: перед серией вычислений с привлечением «форсированной» арифметики одну из точек стоит просчитать «на тихом ходе» и сравнить результаты с «быстрым ходом».

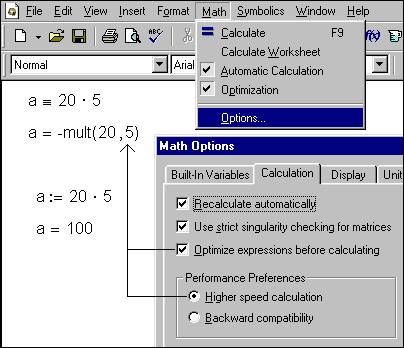
Ошибка «быстрой» математики при оптимизации численных расчетов

Рис. 2b. Ошибка «быстрой» математики при оптимизации численных расчетов

Ускоренную арифметику Mathcad можно отключить – см. кнопку Backward compatibility (совместимость со старыми версиями). Эта возможность («возвращение к старому») реализует известный принцип «Не до жиру – быть бы живу!»: разработчики Mathcad оставили и «крейсерскую» («нефорсированную) скорость счета для тех, кому важен сам результат, а не скорость[7]. Кроме того, новый инструмент часто содержит ошибки. Одна такая ошибка показана на рис. 2b: переменная, введенная глобальным присваиванием, неадекватно ведет себя при умножении, когда одновременно включены режимы Optimize и High speed calculation.

Хорошее правило – при создании нового Mathcad-документа ускоренную математику стоит отключить не только во избежании возможных ошибок («Не до жиру – быть бы живу!»), но и для более точной локализации ошибок. На рис. 2c показана типичная ошибка, какую часто допускают неопытные пользователь Mathcad: индексным переменным присваивают не текстовый (C.вх ® С_вх), а числовой (C[вх ® С_вх) индекс. Пакет Mathcad с ускоренной математикой не указывает, какая именно переменная не определена в выражении (верхняя часть рис. 2c). После отключения ускоренной математики (нижняя часть рис. 2c) все встает на свои места.

Рис. 2с. Ошибка «быстрой» математики при оптимизации численных расчетов

С другой стороны режим ускоренной математики более правильно реагирует на решение «нерешаемой» системы алгебраических уравнений – см. рис. 2d.

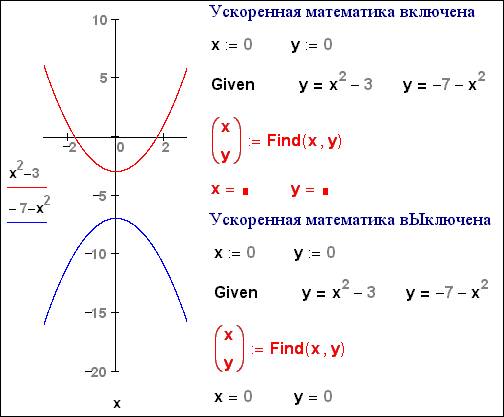
Рис. 2d. «Ошибка» «медленной» математики при решении систем алгебраических уравнений

На рис. 2d в среде Mathcad 2000 и в среде Mathcad 2001 с форсированной математикой выдается неправильный ответ – значения x и y первого приближения. Mathcad 2001 с «крейсерской» математикой правильно реагирует на «нерешаемую» систему – выдает «никакой» ответ.

Режим ускоренной математики позволяет также исправлять некоторые ошибки программирования за счет компиляции программы, что проиллюстрировано рис. 2e:

Рис. 2е. Ошибка, выявленная в программе при ее компиляции

На рис. 2e показано, как при создании программы (численное решение задачи Коши методом Эйлера) в нее был вставлен лишний оператор, изменяющий значение параметра в цикле for. «Медленная» математика Mathcad такой ошибки не «заметит», что не скажешь о «быстрой» математики.

3. Проверка на сингулярность

В жаргонной речи проверку такого рода часто называют, пардон, «проверка на вшивость». У опытных пользователей не только Mathcad, но и других вычислительных систем есть набор примеров «ставящих эти вычислительные системы на место». Мол, как та система умно и быстро не считает, но у меня в запасе есть примерчики, которые лишний раз показывают, что человек (то бишь, я) все равно остается царем не только живой, но и неживой природы. Если вернуться к оптимизации вычислений через аналитическое преобразование, проиллюстрированное на рис. 2а, то можно показать, что такая оптимизация может не ускорять, а замедлять расчеты. Конкретный пример – определенный интеграл, где верхний и нижний пределы равны. Человек и вычислительная математика Mathcad сразу «сообразят», что такой интеграл равен нулю. Символьная же математика Mathcad сначала будет «долго и упорно» искать первообразную подынтегрального выражения и только потом (при подстановке пределов) «сообразит», что никакой первообразной искать не следовало бы. Этот пример позволяет обрисовать особенности «человеческого» и машинного счета: опытному математику часто бывает достаточно беглого взгляда, чтобы решить задачу – понять, например, что это уравнение не имеет корней, а данная матрица вырождена (сингулярна) и т.д. и т.п. Такими примерами пользователи математических пакетов «тыкают в нос» разработчиков, упрекая их в огрехах.

Сингулярная матрица лежит у пользователей компьютеров под рукой в буквальном смысле слова – это кнопки на числовой («маленькой») клавиатуре компьютера. Эту матрицу пользователи Mathcad часто «подсовывают» пакету, прося его вычислить обратную матрицу – см. первый оператор на рис. 3:

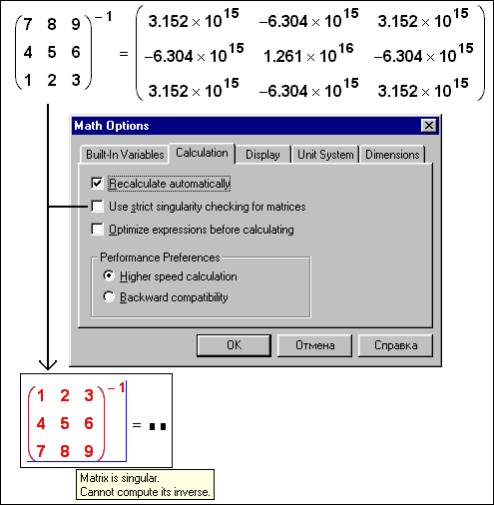
Рис. 3. Работа с сингулярной матрицей

Обычный Mathcad к своему «стыду» вычислит матрицу, обратную сингулярной[8]. В среде Mathcad 2001 эта операция может предваряться «проверкой на сингулярность – Use strict singularity checking for matrices» (cм. рис. 3). В этом случае вычисление обратной матрицы будет прерываться сообщением об ошибке (см. последний оператор на рис. 3 [9]). Аналогичное сообщение, кстати, появляется и в «старом» Mathcad’е при попытке вычисления обратной матрицы средствами символьной математики. Символьная математика Mathcad, вернее, Maple тоже делает ошибки – см. рис. 3a.

Рис. 3a. Ошибка символьной математики

Аналитическая «проверка на вшивость» (еще раз, прошу простить за жаргонное выражение) применяется теперь и к скалярным вычислениям. Пример – х • lg(x) при х = 0. Раньше Mathcad выдавал тут нулевой (ошибочный) ответ, а теперь (Mathcad 2001) – сообщение об ошибке (“This Function is undefined at one or more of points you specified”).

Но в отношении всех этих «ошибок» разработчиков вычислительных систем можно, ну если не оправдать, то хотя бы понять. В среде Mathcad 2001, например, осталась такая ошибка: sin(0)/0 дает ноль в ответе, а не сообщение об ошибке («Деление на ноль»). Дело в том, что в целях того же ускорения расчетов (см. пункт 2) считается, что произведение[10] равно нулю, если равен нулю первый сомножитель.

Разработчики Mathcad, создавая компьютерную арифметику, зажаты между требованиями точности, безошибочности и быстродействия и требованиями разумности системы с точки зрения ее стоимости и сроков создания. Да, можно выпустить на рынок безупречный программный продукт, «безупречность» которого будет достигнута за счет его очень высокой цены и низкого быстродействия. Такой продукт может не найти своего покупателя.

Пример с сингулярной матрицей высвечивает нам очень интересную тенденцию в развитии вычислительных систем: вычислительные системы должны уметь не только решать поставленные задачи с приемлемой точностью и с приемлемой скоростью, но и уметь делать предварительный анализ решаемой задачи.

В трех приведенных выше примерах проиллюстрированы три направления развития Mathcad:

1. Качественные изменения: оператора не было, а в новой версии он появился (рис. 1).

2. Количественные изменения: скорость счета возросла (рис. 2)

3. Исправление ошибок или снятие некоторых ограничений. Третье направление относится и к четвертой новинке Mathcad 2001.

4. Размерные величины в программах.

В среде Mathcad 2001, как уверяют разработчики, решена проблема размерных величин в циклах, альтернативах и других конструкциях, изменяющих естественный порядок выполнения операторов.

В средах Mathcad 6-2000 Pro[11] в плечах альтернативы допустимо было иметь величины одного типа – либо безразмерные, либо одной размерности. Отклонение от этого правила прерывалось сообщением об ошибке – см. первую половину рис. 4, где показана работа функции if и оператора if. В среде Mathcad 2001 это ограничение снято (см. вторую половину рис. 4).

"Размерная" альтернатива в Mathcad

Рис. 4. "Размерная" альтернатива в Mathcad

Сложнее обстояло дело с оператором return, досрочно прерывающим выполнение программы.

Исправления в работе функции return

Рис. 5. Исправления в работе функции return

На рис. 5 показано создание и работа функции, возвращающей либо периметр, либо площадь треугольника в зависимости от значения четвертого аргумента (первые три аргумента – длины сторон треугольника). Mathcad – 2000 Pro путается в этих трех сторонах треугольника «как в трех соснах». Первоначально в среде Mathcad 2000 Pro программно-созданная функция возвращала правильный числовой ответ (2.92 и 0.369, если говорить об условиях задачи, показанных на рис. 5), но неверные единицы измерения для периметра (m² вместо m). В июле 1999 г. появилась «заплатка» С (вторая заплатка для Mathcad 2000 Pro), которая привела к тому, что функция на рис. 5 вообще перестала выдавать размерные величины при размерных исходных данных. В среде Mathcad 2001 данная ошибка устранена. Но все равно недоработки остались. Так по-прежнему параметр цикла не может принимать значения различных физических величин – см. рис. 6.

Рис. 6. Ошибка или ограничения при работе с размерностями в цикле Mathcad

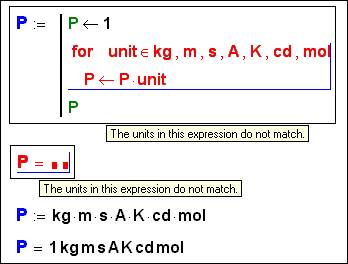
Это, по-видимому, связано с тем, что считается (задумано так), что цикл с параметром в среде Mathcad выбирает значение для параметра цикла из вектора. А вектор (массив) – это собрание сугубо однотипных (одноразмерных) элементов. Но на рис. 6 нет никакой физической крамолы (высчитывается произведение всех семи основных единиц SI), но, тем не менее, выполнение программы прерывается сообщением об ошибке. Использование единиц измерения физических величин в программах тормозится и тем, что программы очень часто работают с векторами и матрицами, которые по-прежнему могут хранить только безразмерные или «равноразмерные» величины.

На рис. 6 использован недокументированный прием – задание параметров цикла for в виде списка. Документация Mathcad разрешает тут использовать только переменную области (Range Variable) или вектор. На рис. 6a показано, какие последствия могут произойти при опоре на данный недокументированный прием.

Рис. 6a. Особенности цикла for в среде Mathcad 2001

На рис. 6a программным способом рассчитывается произведение первых семи простых чисел. Переменная цикла for принимает значение из списка (2, 3, 5, 7, 11, 13,17) – из ряда чисел, разделенных запятыми. В среде Mathcad 2000 этот недокументированный прием не давал сбоев, а в среде Mathcad 2001 – перестал работать самым «нехорошим» манером: неправильный ответ (нуль вместо положенных 58) без какого-либо сообщения об ошибке. Приходится заменять список на вектор-строку. Но вектор-строка – это не вектор, а матрица с одной строкой. Выходит так, что мы опять используем недокументированный прием: вектор (2 3 5 7 11 13 17) нужно развернуть на 90 градусов (транспонировать).

Первая «заплатка» к Mathcad 2001 (та, что добавляет к лицензионному номеру букву A – см. рис 11) описанную ошибку (невозможность работы со списком в цикле for) исправляет

Кстати, мало кто знает, а еще меньше кто пользуется таким приемом – в среде Mathcad параметр цикла for может быть не только целым числом (счетчик цикла) и не только действительным числом, но и комплексным числом (см. рис. 6b) и даже вектором – простым (см. рис. 6с) или даже составным.

Рис. 6b. Параметр цикла – комплексное число

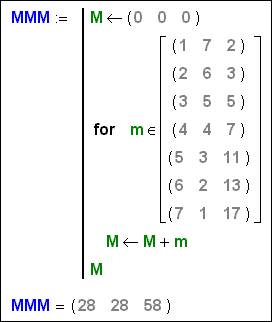
Рис. 6c. Параметр цикла – вектор

5. Новые функции

5.1. Координатная система графиков

В среде Mathcad 2000 появилась возможность менять систему координат трехмерного графика с прямоугольной (картезианской) на цилиндрическую и сферическую. Эта смена координат велась и ведется через радиокнопки закладки General диалогового окна форматирования трехмерного графика. Автор использовал эту возможность для рисования сложных объемных фигур («яблоко» и «ваза») по простым формулам – см. галерею трехмерной графики Mathcad – http://www.mathsoft.com/mathcad/library/3Dplots/).

В среде Mathcad 2001 преобразование координат графиков можно делать не только визуально, но и «математически» с помощью новых функций, возвращающих координаты точек в новой системе координат: sph2xyz(v), sph2xyz(r, q, f), cyl2xyz(v), cyl2xyz(r, q, f), xyz2sph(v), xyz2sph(r, q, f), xyz2cyl(v), xyz2cyl(r, q, f), pol2xy(v), pol2xy(r, q, f), xy2pol(v) и xy2pol(r, q, f).

5.2. Новая «сглаживающая» функция

В Mathcad (начиная с 7-й версии, если автор не ошибается) есть функция genfit, позволяющая решать задачу общего («генерального» – general) сглаживания (fitting). Общего в том смысле, что сглаживающим (аппроксимирующим) уравнением теоретически может быть уравнение любого вида с любым числом искомых коэффициентов.

Но для многих пользователей Mathcad эта функция остается некоей «китайской грамотой» с непонятным смыслом и способом вызова. Функция genfit требует в качестве аргумента не только саму сглаживающую функцию с аргументами-элементами вектора, но и частные производные этой функции по различным искомым коэффициентам. В среде Mathcad 2000 функцию genfit «рассыпали» на ряд функций, решающих аппроксимационную задачу по отдельным функциям: expfit(vx, vy, vg), lgsfit(vx, vy, vg), logfit(vx, vy, vg), pwrfit(vx, vy, vg) и sinfit(vx, vy, vg), где сглаживающая функция имеет вид: a*e^(b*x)+c, a/(1+b*e^(-c*x)), a*ln(x+b)+c, a*x^b+c и a*sin(x+b)+c, соответственно. В Mathcad 2001 этот ряд дополнен новый функцией lnfit(x, y) (сглаживающая функция – a*ln(x)+b). Работа функции lnfit(x, y) показана на рис. 7.

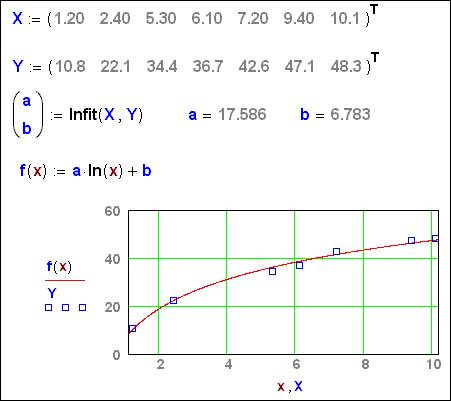
Работа новой аппроксимирующей функции

Рис. 7. Работа новой аппроксимирующей функции

Сглаживающих функций придумать можно очень много. Автор не может запомнить, какие из них встроены в Mathcad , а какие нет. Он поступает проще – см. рис. 7a, где реализован механизм аппроксимации функцией любого вида с любым числом коэффициентов. Можно посоветовать фирме MathSoft не вводить новые частные функции аппроксимации, а разработать и встроить в Mathcad универсальный инструмент аппроксимации. Например, такой, какой показан на рис. 7a.

Универсальная аппроксимация с помощью функции Minimize

Рис. 7a. Универсальная аппроксимация с помощью функции Minimize

В Mathcad 2001 встроены и другие новые функции. Автор их не анализирует, а только перечисляет:

5.3. Волновые функции работы с файлами

READWAV(“F”), WRITEWAV(“F”, s, b) и GETWAVEINFO(“F”)

5.4. Новая функция построения гистограммы

histogram(n, y)

6. Новые возможности интерфейса

Одно из самых слабых мест Mathcad – это его интерфейс. Пользователь, чтобы ввести в расчет какое-либо значение, должен через клавиатуру набирать числа и тексты, которые операторами «:=» или «º» присваиваются нужным переменным: A :=24.12, B º”MathSoft Engineering and Education[12]” и т.д. Это уже давно перестало соответствовать новым стандартам «визуального» интерфейса, когда нужные данные вводятся в расчет простым щелчком мыши.

В среде Mathcad 2001 наконец-то появились новые возможности по организации современного интерфейса пользователя, позволяющие вводить в Mathcad-документ стандартные управляющие конструкции (рис. 8): «галочку» (CheckBox), список (ListBox), кнопку (PushButton), радиокнопку (RadioButton), бегунок (Slider) и текстовое окошко (TextBox).

Рис. 8. Новые компоненты интерфейса Mathcad

На рисунках ниже даны примеры работы трех новых элементов интерфейса «галочки» (CheckBox – рис. 8a), списка (ListBox – рис. 8b),и бегунка (Slider – рис. 8c)

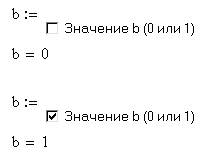
Рис. 8a. Ввод значения переменной с помощью «галочки»

Рис. 8b. Ввод значения переменной из списка

Рис. 8c. Ввод значения переменной с помощью «бегунка»

7. Mathcad и Internet

7.1. Гипертекстовый переход к отдельным формулам

Эта возможность появилась еще в последнем обновлении Mathcad 2000 – у операторов Mathcad можно ставить метку, к которой затем можно делать переход – см. рис. 9.

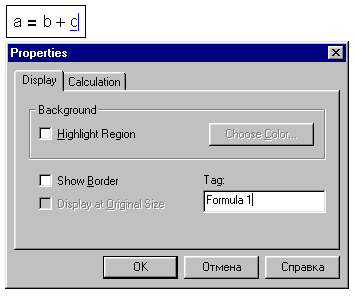
Рис. 9. Метка у оператора Mathcad

7.2. Сохранение Mathcad-документов в формате MathML

У Mathcad 6-2000 были проблемы с публикацией решений в сети Internet: формат HTML «держал» формулы в виде рисунков. В среде Mathcad 2001 эта проблема решена – см. рис. 10.

MathML – язык разметки, созданный на основе XML (Extensible Markup Language), предназначенный для генерации математических формул. В ближайшие несколько лет XML должен будет заменить HTML. Первые стандарты XML появились в прошлом году. Информация на www.w3.org или http://citforum.indi.ru/internet/xml/links.shtml.

Рис. 10. Новые возможности по сохранению Mathcad-документа

7.3. Информация о новых «заплатках»

Вот типичный упрек в адрес пакета. «Не прошло месяца с момента выхода в свет новой версии Mathcad, а фирма-разработчик предлагает скачать со своего сайта программу-заплатку (Patch, UpDate) – см. http://www.mathcad.com/upgrade). Это знак того, что разработчики в погоне за прибылью выбрасывают на рынок сырой программный продукт (полуфабрикат), а затем досылают пользователям пресловутые «заплатки», которые еще не известно, как[13] будут работать в программе, но доверие к ней снизят – это уж точно». Возражение на этот упрек можно построить так. Дело не в ошибках, которые, увы, неизбежны в любых программах, а в отношении разработчиков к ошибкам. Об ошибках, замеченных пользователями и разработчиками после выхода программы в свет, можно молчать 2-3 года до выхода новой версии программы. Так поступают многие фирмы. А можно эти ошибки сразу исправлять через свободно распространяемые «заплатки». Аналогичная ситуация наблюдается в автомобилестроении. Некоторые фирмы предпочитают отзывать на доработку свои новые автомобили. Здесь также можно спорить о том, повышают или понижают авторитет фирмы данные акции.

В меню Help Mathcad 2001 появилась новая команда Mathcad Update (рис. 11), позволяющая узнать, появилась ли новая «заплатка» Mathcad без выхода из этой программной среды.

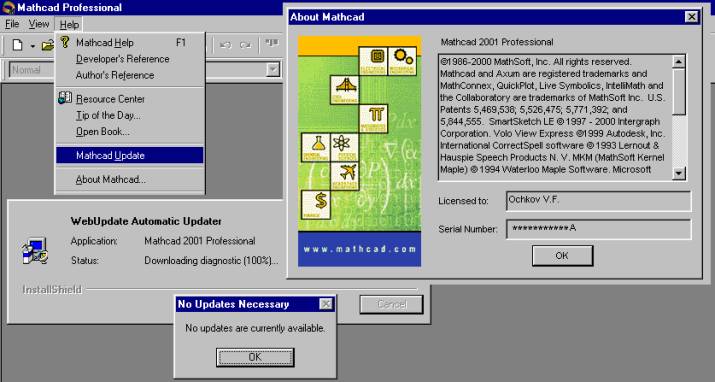
Автоматическое обновление Mathcad

Рис. 11. Информация о новых «заплатках»

Из рис. 11 видно, что a) данная версия Mathcad подправлена «заплаткой» A (первой – см. серийный номер); b) новых заплаток пока нет. Примечание: в июле 2001 г. появилась заплатка B.

Резюме

Честно говоря, пользователи Mathcad несколько устали от таких частых появлений новых версий этой программы. Пользователи только-только освоились с 2000-й версией, как ей на смену спешит Mathcad 2001. Фирме MathSoft Engineering & Education, Inc. неплохо сделать паузу. Российские пользователи, правда, не так сильно страдают от такой частой смены «Mathcad-эпох» – на «пиратских» лотках в Москве («на Горбушке» – см. http://twt.mpei.ac.ru/ochkov/mc8Pro.book/6_text.htm#_Toc471716598) Mathcad-2001 появился еще раньше чем в Америке (см. фото типичного московского компьютерного лотка). Законопослушным (и не таким нищим) пользователям приходится раскошеливаться на 500 баксов…

Беда еще и в том, что частая смена версий Mathcad никак не способствует «лечению» этой программы от такой хронической ошибки:

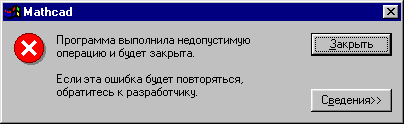
Мотивом выхода в свет Mathcad 2000 был, естественно, сам 2000 год – год, когда на компьютерный рынок «как из мешка» были высыпаны программные продукты с суффиксом «2000»: Windows 2000, Office 2000, AutoCAD 2000 и др. Из переписки с сотрудниками MathSoft автор выяснил, что у Mathcad 2001 три таких мотива появления:

1. Полная адаптация к Windows 2000

2. Необходимость сохранения Mathcad-документов в формате MathML (см. рис. 10)

3. Прибамбасы[14], главный из которых – это новая машинная математика (см. рис. 2)

Что потеряли?

Mathcad 2001 не только что-то приобрел, но и что-то … потерял. И это тоже нужно отметить, говоря о новинках Mathcad.

Пакету Mathcad чего-то, естественно, не хватает[15], но и что-то у него есть лишнее. Это «лишнее» образуется разными путями. Во-первых, в среде Mathcad появляются новые функции и операторы, дублирующие старые, и это мы уже отметили, описывая, например, новый оператор деление «¸» (см. рис.1) и «критикуя» оператор genfit, который не прижился в среде Mathcad и «рассыпался» на ряд функций с суффиксом fit. Не «прижилась», вернее, «отмерла» функция until (цикл с предпроверкой с одним оператором в теле) – ее «выдавил» оператор (процедура) while: в среде Mathcad 2000 и 2001 функции until уже нет в Мастере функций, но сама функция пока работает для обслуживания Mathcad-документов, созданных в ранних версиях этого пакета.

Некоторые потери могут заметить только «продвинутые» пользователи – сравните рис. 12 и рис. 13.

Рис. 12. Проверка имен на «свободность» в среде Mathcad 2000

Рис. 13. Проверка имен на «свободность» в среде Mathcad 2001

Но некоторые инструменты Mathcad исчезают очень даже заметно. Такая судьба постигла утилиту MathConnex, появившуюся в седьмой версии Mathcad – в среде Mathcad 2001 ее уже нет. Утилита MathConnex была задумана как средство интеграции (соединения – Connex) различных математических программ (Math – Excel, MatLab и, естественно Mathcad) с возможностью перекачки данных между ними. Но MathConnex, как говорится, не пошел. Одна из причин в том, что файлы, создаваемые в среде MathConnex, очень объемные: простенькая задача «тянет» на несколько Мбайт дискового пространства. Так или иначе, но в среде Mathcad 2001 утилиты MathConnex уже нет.

И последнее.

Новинки каждой версии Mathcad можно разделить на две группы: новинки в самой «математике» пакета (Math) и новинки в сервисных инструментах (условно говоря, CAD – computer-aided design).

Прослеживая главные, по мнению автора, новинки в математике Mathcad, можно отметить следующее:

· пятая версия – команды символьной математики

· шестая версия – инструменты программирования

· седьмая версия – операторы символьной математики

· восьмая версия – функции решения оптимизационных задач с ограничениями

В 2000-й и 2001-й версиях Mathcad «математические» изюминки увидеть, а тем более выделить довольно трудно. Если 2000-я версия Mathcad вписывалась в общую тенденцию, тогда всякая уважающая себя компьютерная фирма считала своим долгом выпустить на рынок программный продукт, отмеченный магической датой «2000», (см. выше), то «математические» мотивы появления 2001-й версии совсем туманны.

[1] См. предисловие к данной серии.

[2] Альфа-версия тестируется на фирме-разработчике, бета-версия рассылается так называемым бета-тестерам, а гамма-версия – это конечный (коммерческий) продукт, который уже «тестируется» всеми пользователями. Результаты такого теста выливаются в разного рода «заплатки», подправляющие программу.

[3] Под спецсимволами мы будем понимать те символы (+, – , пробел, _*, /, $, @ и т.д.), которые еще со времен DOS-версий Mathcad были зарезервированы для ввода операторов (арифметические операторы, суммирование, построение графиков и т.д.).

[4] Это не совсем так: оператор деления с единичным числителем и оператор обратного числа могут возвращать одинаковый результат, но работать по разным алгоритмам.

[5] Мечта многих пользователей Mathcad, которая, увы, не реализована в среде 2001 – это возможность компиляции Mathcad-документа в exe-файл, например, который можно было бы запускать без самой среды Mathcad.

[6] Автор иногда по этому времени оценивает работу студентов – сам ли он решил задачу или списал ее у товарища.

[7] Можно предположить, что «форсированная» арифметика не совсем полностью протестирована и может давать сбои.

[8] Это относится к вычислительной математике.

[9] Здесь уже использовалась не «компьютерная», а «телефонная» вырожденная матрица. Непонятно, почему «компьютерщики» и «телефонщики» не могут договориться о единообразии. Это тем более странно, если принять во внимание, что скоро мобильный телефон практически не будет отличаться от компьютера.

[10] Арифметика Mathcad не «обучена» делению: деление – это умножение числителя на обратный знаменатель.

[11] Приставка Pro (Professional) означает то, что тут возможно и программирование.

[12] Новое название фирмы – разработчика Mathcad (с января 2001).

[13] Иногда можно четко зафиксировать такие исправления ошибок (см. совет 2).

[14] Мой машинный переводчик перевел это слово как «Add On», но русское слово «прибамбасы» более точно отражает суть изменений.

[15] Автор такого рода “хотелки” собрал на в минифоруме Mathcad ММ (ст. – ...) форума Collaboratory (… , описание форума …)