УГАДАЙ ОБРАЗ
Журнал Информатика в школе, №9 (73) 2011 г.
Была такая
телевизионная игра «Угадай мелодию»[1].
Проигрывались первые звуки какого-нибудь музыкального произведения, а выигрывал
тот, кто первым называл его.
Эту игру можно перевести в визуальную плоскость и
назвать «Угадай образ» или, если быть более точным, «Угадай человека по его
портрету». Портрет человека в этой игре нужно показывать на экране не весь
сразу, а как мелодию – отдельными последовательными нотами, пардон, отдельными
точками (элементами растра), постепенно заполняющими экран. И чем больше точек
будет показано, тем больше вероятность узнать образ. Ниже приведена и описана
программа для математического пакета Mathcad, которая проигрывает эту «портретную мелодию».
Портрет человека, отображаемый на мониторе компьютера[2], да и любое другое изображение – это, как правило, множество разноцветных точек. Такое изображение с точки зрения математики – это матрица, элементы которой хранят числа от 0 до 255, например. В последнее время бурно развивается направление в информационных технологиях, связанное с опознаванием образов.
Два типичных примера практического использования
достижений в этой науки: камера наблюдения фотографирует автомобиль,
превысивший скорость на дороге, а компьютер обрабатывает этот снимок, определяет
марку и номер госрегистрации этого автомобиля и
штрафует нарушителя; при паспортном контроле на границе цифровая фотокамера
фиксирует лицо и/или радужную оболочку глаза контролируемого, а компьютер
сравнивает их с теми данными, какие «вшиты» в предъявленный паспорт.
Описываемая в данной статье игра «Угадай образ» не
только поможет нам развлечь друзей на вечеринке интересным конкурсом, но и
приоткроет некоторые секреты современных технологий распознавания образов.
На рис. 1 можно видеть «разыгрывание» одного из
самых узнаваемых образов – портрета Че Гевары[3],
смотрящего на нас с многочисленных плакатов и теннисок.
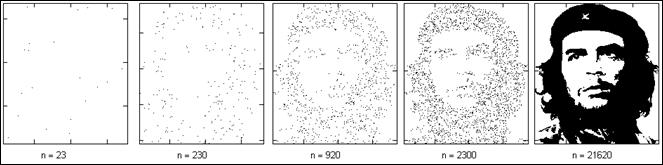
Рис. 1. Точечное рисование портрета Че Гевары
Портрет Че Гевары состоит из 21 620 черных точек[4]
на белом фоне. На рис . 1 он прорисован разным количеством точек (n): при n = 230 нашего героя еще
не узнать, а при n = 920 можно уже
поднимать руку и кричать: «Я узнал его!».
Портрет рисуется так. В интернете
отыскивается данный портрет Че Гевары[5]
и сохраняется на диске в черно-белом формате bmp-файла – см. рис. 2.
Рис. 2. Поиск портрета в Интернете и сохранение его на диске
На рис. 2 показан поиск с помощью поисковика Google портрета Че Гевары в Интернете и сохранение его на диске с помощью
команды меню, появляющейся при нажатии правой кнопки мыши. Портреты можно не
только выуживать из Интернета, но и делать самому – фотографировать друзей
и близких на цифровую камеру, а файлы сохранять на диске для дальнейшей их
обработки.
В среде математической программы Mathcad [1] есть команда вставки
в расчет рисунка (рис. 3), отдав которую и указав имя файла, можно
нарисовать в Mathcad-документе
выбранную картинку.

Рис. 3. Вставка картинки в Mathcad-документ
Вставка картинки в Mathcad-документ – это
сам по себе очень полезный инструмент. С помощью функции if (если) можно менять имя файла и подгружать
ту или иную картинку в зависимости от расчетной ситуации.
Черно-белую картинку, хранящуюся на диске в виде
bmp-файла, можно превратить в матрицу,
элементы которой будут фиксировать цвет точки изображения: 0 – черный и
255 – белый. Для этого в среде Mathcad есть функция READBMP – см. рис. 4.

Рис. 4.
Преобразование картинки в матрицу
На рис. 4 мы «распечатали» правый нижний угол
матрицы M, чтобы показать, в каком виде будет храниться в матрице левое плечо Че Гевары. В матрице M 207
строк и 189 столбцов, хранящих информацию о 39 123 точек портрета. На
рис. 4 показано, как с помощью функций rows и cols подсчитано количество рядов и
столбцов матрицы M.
Если у нас есть матрица – собрание чисел, сгруппированных
по рядам[6]
и столбцам, то с ней можно многое чего делать: класть на бок (в математике это
называется транспонирование матрицы), переворачивать, сортировать и т.д. Если
матрица квадратная, то такую матрицу можно инвертировать (вычислять обратную
матрицу, перемножение которой на исходную даст единичную матрицу – матрицу с
единицами по главной диагонали и с нулями в остальных местах); у такой матрицы
можно вычислить определитель и т.д. и т.п.
Мы же нашу матрицу разложим на два вектора с именами
Ion и Iat, которые будут хранить
координаты черных точек нашего черно-белого портрета Че
Гевары. Это делается в первой программе, показанной
на рис. 5, двумя циклами for,
перебирающими матрицу по столбцам и рядам. Если очередной элемент матрицы M
будет равен нулю (черная точка портрета), то в вектор X будет записан номер
данного столбца, а в вектор Y номер ряда.
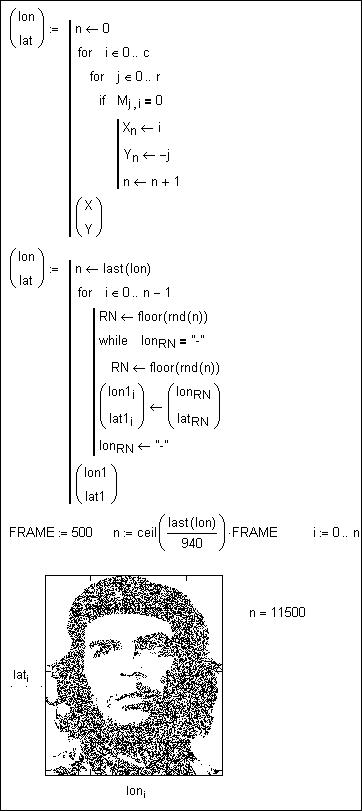
Рис. 5. Преобразование матрицы в два вектора
Вторая программа, показанная на рис. 5, ядром
которой является функция rnd, возвращающая
случайные числа, перемешивает элементы векторов Ion
и Iat.
После этого несложно средствами анимации Mathcad [2] поточечно
рисовать нашего героя – см. его прорисовывающийся
портрет на рис. 5. Если же векторы Ion
и Iat
не перемешать, то картинка будет выдаваться на экран компьютера построчно и
можно четко видеть растры изображения. Так тоже можно вести игру «Угадай
образ».
Программы и анимации, описанные в данной статье,
лежат на сайте владельца Mathcad – компании PTC [3]. С этого же сайта можно
скачать бесплатную пробную версию пакета Mathcad 15.
Литература и Интернет-источники:
-
Очков В.Ф. Mathcad 14 для студентов и инженеров: русская версия. Издательство БХВ-Петербург, 2009 (http://twt.mpei.ac.ru/ochkov/Mathcad_14/RusIndex.html)
-
Очков В.Ф. Живые кинематические схемы в Mathcad // Информатика в школе (на рецензии – http://twt.mpei.ac.ru/ochkov/Mathcad-15/kinematic.html)