История одного шедевра
(Mathcad и нестандартная графика)

Валерий Очков http://twt.mpei.ac.ru/ochkov

(Английская версия статьи)

(Отзывы на статью)

Слово «шедевр» в названии статьи, конечно, должно быть взято в кавычки. Ведь заголовок статьи – это ни что иное, как название серии TV-передач, в которых рассказывается об истории создания известных полотен, хранящихся в Третьяковской галерее (http://www.tretyakov.ru), в Эрмитаже (www.hermitage.museum.ru), в Русском музее (www.rusmuseum.ru) и в других местах. 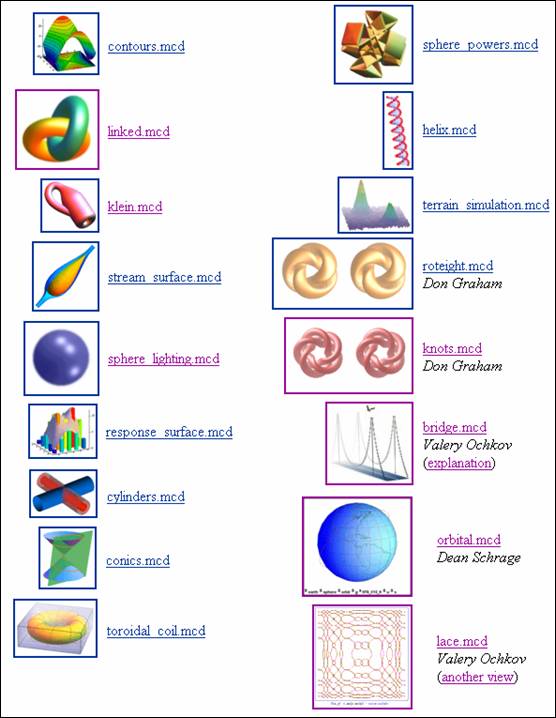Наш «шедевр» также хранится в галерее, но не в простой, а в виртуальной – в галерее необычной трехмерной графики, созданной с помощью Mathcad[1] (рис. 1).

Рис. 1. Галерея необычной графики, созданной в сред Mathcad (на январь 2000 г.)

Адрес галереи в Internet: http://www.mathcad.com/resources/gallery.

А история «шедевра» (он в правом нижнем углу на рис. 1 и назван lace.mcd) такова.

Одна из рутинных задач, решаемых в среде Mathcad, это поиск корней алгебраических уравнений. К этой проблеме очень часто сводятся разного рода физические, химические, экономические и прочие «предметные» задачи, когда требуется свести какие-либо балансы (сил, масс, количеств вещества, сумм денег и т.д. и т.п.). Mathcad имеет довольно мощный встроенный инструмент решения и верификации (проверки) подобных задач – линейных и нелинейных, безразмерных и включающих размерные величины (метры, килограммы, рубли и т.д. и т.п. – см. статью Mathcad и размерность физических величин).

Рис. 2. Аналитическое решение системы двух алгебраических уравнений

На рис. 2 показано, как с помощью средств символьной математики Mathcad были найдены все 24 корня системы двух нелинейных алгебраических уравнений вида:

x²×y^2_ 7×x³×y^3_7=0

(x²+y²)^2_7×(x^2_y²)=0

Из найденных корней четыре (1-й, 6-й, 19-й и 22-й, если считать сверху[2]) действительные, остальные – мнимые (комплексные). С решением, показанным на рис. 2, нам, можно сказать, повезло: стоит слегка усложнить одно из уравнений системы, как символьная математика Mathcad откажется решать задачу. Оператор solve (решить), задействованный в задаче на рис. 2, – это своего рода максималист, возвращающий либо все решения системы, либо ни одного. Человеку же, сидящему за компьютером, как правило, нужен один действительный корень вблизи точки, указанной самим пользователем.

Рис. 3. Численное решение системы двух алгебраических уравнений

На рис. 3 действительные корни нашей системы ищутся средствами уже не символьной, а вычислительной (приближенной) математики Mathcad: встроенная функция Find возвращает значение своих аргументов (x и y), превращающих уравнения системы (они записаны ниже ключевого слова Given и выше функции Find) в тождества. Вернее, делающих отклонение левых и правых частей уравнений системы меньше (по модулю) чем значение встроенной переменной TOL (TOLerance, погрешность – по умолчанию она равна 0.001). Отсюда становится понятным, почему у термина «вычислительная математика» есть синоним – «математика приближенных вычислений». Тут подразумевается, что символьная (аналитическая) математика, задействованная в решении задачи на рис. 2, – это математика абсолютно точных вычислений. Вот поэтому-то, а также из-за того, что символьная математика пытается всегда выдать все решения, она бессильна перед более-менее сложной задачей. Но человеку, как правило, не нужны абсолютно все абсолютно точные ответы (рис 2). Он обычно удовлетворяется приближенными ответами по одиночным корням (рис. 3).

Бог любит троицу. Полное решение задачи в среде Mathcad должно включать не только символьное[3] (рис. 2) и не только приближенное (рис. 3), но и графическое решение, которое не только визуализирует задачу, но и подтверждает правильность ее решения (верифицирует). Графическое решение нашей задачи – это вычерчивание на декартовом графике двух кривых, точки пересечения которых будут действительными корнями системы. Сложность тут лишь в том, что не всегда удается преобразовать систему (см. пример выше) к виду, готовому для построения декартовых графиков в среде Mathcad:

y1(x) := f1(x)

y2(x) := f2(x)

Здесь нужно будет средствами символьной математики попытаться решить уравнения f1(x, y) = 0 и f2(x, y) = 0 относительно x, что само по себе является довольно сложной задачей, которая очень часто просто не решается. А если исходное уравнение и решается, то и решений может быть много – y1₁(x), y1₂(x), … y1_N(x)… y2₁(x), y2₂(x)… y2_N(x), каждое из которых требует отдельной кривой на графике. Получается некий гордиев узел, который мы развязывать не будем, а просто… разрубим его[4].

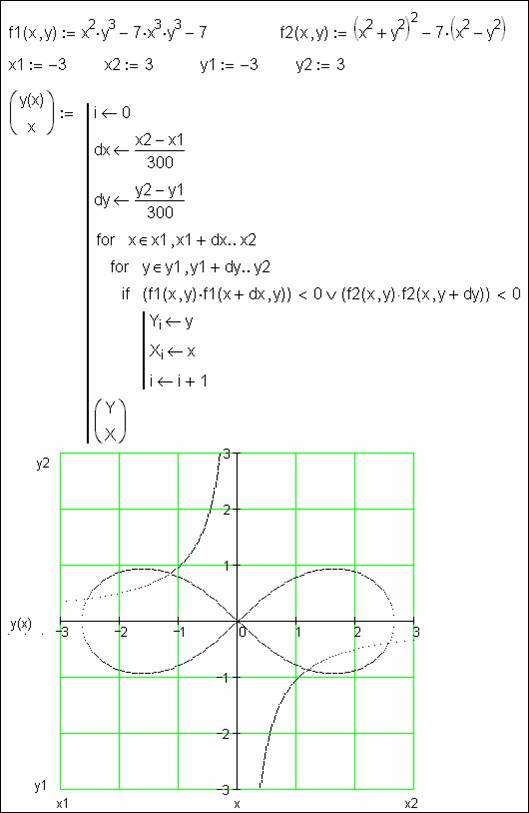
Рис. 4. Графическое решение системы двух алгебраических уравнений

Построение графика функции f(x,y)=0 на MAS (Mathcad без Mathcad – вставка 27 декабря 2003)

На рис. 4 показана универсальная методика графического решения системы двух алгебраических уравнений: поверхность x – y сканируется (перебираются координаты x и y двумя циклами for) и запоминаются точки, где функция f1 или (см. оператор V – оператор логического сложения ИЛИ) функция f2 близка к нулю[5]. В момент прогонки нашей Mathcad-программы на рис. 4 генерируется два вектора y(x)[6] и x одной длины, элементы которых хранят графическое решение нашей задачи: на графике пересечение кривых (в центре знаменитая лемниската[7] Бернулли) – это корни нашей системы. Их можно уточнить, взглянув на рис. 2 и 3, либо изменив значения переменных x1, x2, y1 и y2 (zooming графика).

Вот теперь мы и подобрались к вышеупомянутому «шедевру», выставленному в галерее MathSoft, Inc. (рис. 1).

Как понимает читатель, методика построения графика, показанная на рис. 4, годится и для системы, и для одиночного уравнения вида f(x, y). Тут автору (и этой статьи и методики разрубания гордиевого узла, показанной на рис. 4) попалась на глаза проблема, «выложенная» в форуме Collaboratory (см. статью «Mathcad и Internet, или Сетевой колхоз», КомпьютерПресс, 3’2000 – http://twt.mpei.ac.ru/ochkov/Collab/Collab.htm): один пользователь Mathcad попросил помочь ему построить график уравнения

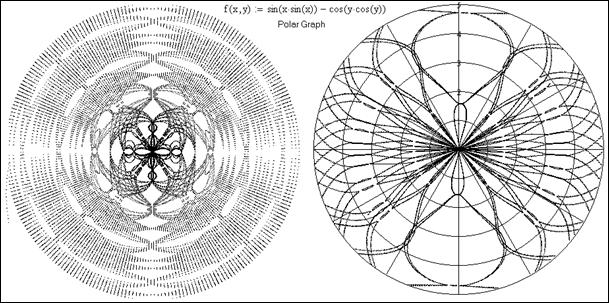
sin(x × sin(x)) – cos(y × cos(y)) = 0.

Стандартные средства Mathcad позволяют решить эту задачу только через построение линий одного уровня (Contour Plot – «контурная карта»). Решение задачи – линия нулевого уровня (f(x, y) = 0 – береговая линия на географической карте). Но беда в том, что по вышеописанному конкретному уравнению четкую линию f(x, y) = 0 получить никак не удавалось – все было как в тумане[8]: видно, что кривая очень сложная, но какая она именно, неизвестно.

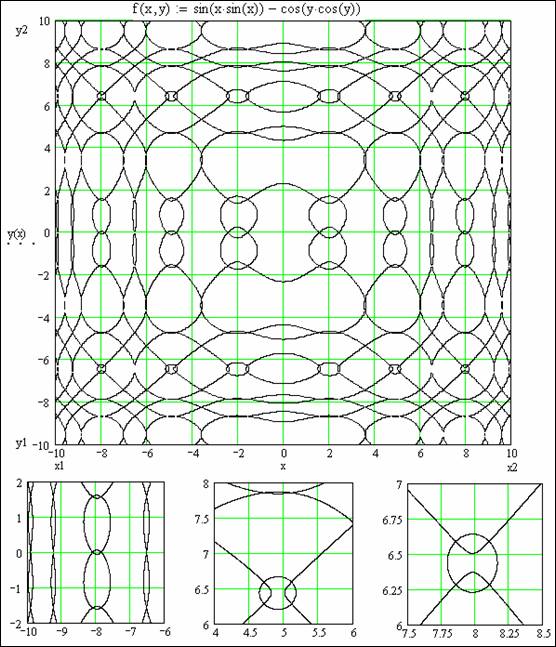
Рис. 5

На рис. 5 наша программа сканирования плоскости x – y из рис. 4 несколько усложнена (продублирована): сканирование ведется не только «по вертикали» (for x … for y …– см. рис. 4), но и «по горизонтали» for y … for x …). Это делается для того, чтобы повысить четкость графиков, которые на рис. 4 разрывались на отдельные точки при малом подъеме по оси y[9].

Программа на рис. 5 работает медленно[10], но верно – на рис. 6 и рис. 7 можно увидеть четкие графики нашей функции, сплетающиеся в кружево (lace). Под этим названием (lace) наше «живописное полотно» и было вывешено в галерее MathSoft, Inc. Получилась квадратная кружевная шаль.

Рис. 6

Рис. 7

На рис. 8 можно увидеть полярные графики нашей функции, также кривые, сплетающиеся в кружево – в кружевную салфетку для круглого стола.

Рис. 8

PS

Методика построения графиков, изложенная выше, после небольшой доработки (см. программу на рис. PS 1) годится для графического отображения не только уравнений, но и неравенств.

Рис. PS 1. Программа для построения вышивки Ришелье – графического отображения неравенства

Изобразительное искусство немыслимо без цвета. Автор расцветил переменные в программе на рис. PS 1:

• черный цвет – встроенные конструкции
• синий цвет – пользовательские переменные и функции
• малиновый цвет – пользовательские формальные переменные
• зеленый цвет – пользовательские локальные переменные

Подробнее идею цвета в Mathcad-программах автор изложил в форуме Collaboratory (сам форум и статья о нем).

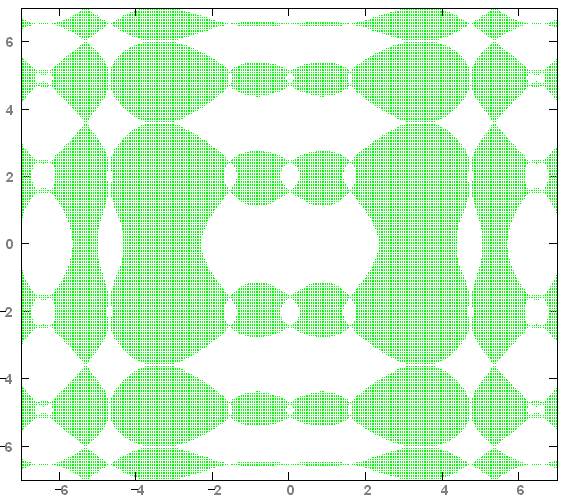
Если график функции можно сравнить с кружевом, то график неравенства похож на другой образец народного творчества – на вышивку Ришелье. Правильнее, но менее красиво сказать, не «на вышивку», а « на вырезку» – на ткани делают «художественные» дырки и обметывают края (см. рис. PS 2). В детстве дома автора окружали такие салфетки – ими мама накрывала все, что можно накрыть: подушки на кровати, шкафы и даже телевизор (КВН-49).

Рис. PS 2. Графическое отображение неравенства – вышивка Ришелье

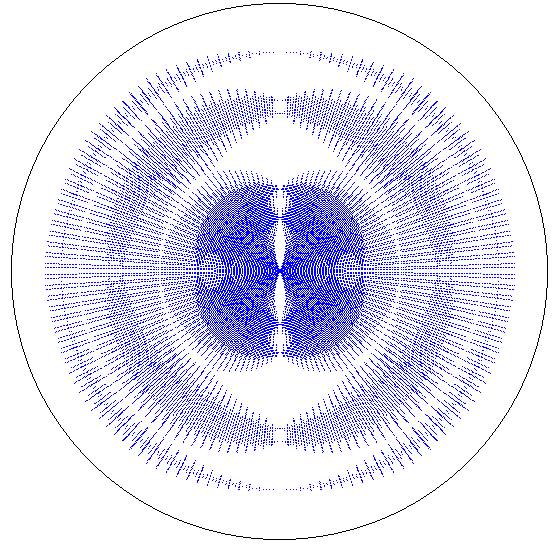
Полярное отображение графика на рис. PS 2) тоже «красиво» – см. рис. PS 3.

Рис. PS 3. Еще одна кружевная круглая салфетка

Предлагаю читателям «интересное задание» – поиск уравнений вида f(x, y) = 0, по которым можно построить «интересные рисунки».

Отзывы на статью:

Уважаемый Валерий Федорович!
Нарисовала Вам эти линии как линии уровня. Посылаю картинки в архиве. Парметрически эти функции разумно задать не удастся, поскольку здесь на самом деле – семейство замкнутых линий у каждой из которых свое параметрическое представление (это связано с тем, что возникают обратные тригонометрические функции, которые не являются периодическими).

С уважением, Н.А.

________________________________________

Здравствуйте господин Очков!

Посылаю Вам пример Lace, но это скорее не кружева, а косы. Данное уравнение связывает интервалы времени и углы эксцентрической аномалии для одного из семейств решения ограниченной задачи трех тел с последовательными столкновениями. По-видимому, впервые получено Henon M. «Sur les orbites interplanetaires qui rencontrend deux fois la terre», Bull. Astron. Ser. 3 1968. T. 3, N 3. P. 377-402.

Время счета для 700 точек, 175.1 сек на Dell Inspiron 7000.

С уважением, Селезнев Сергей.

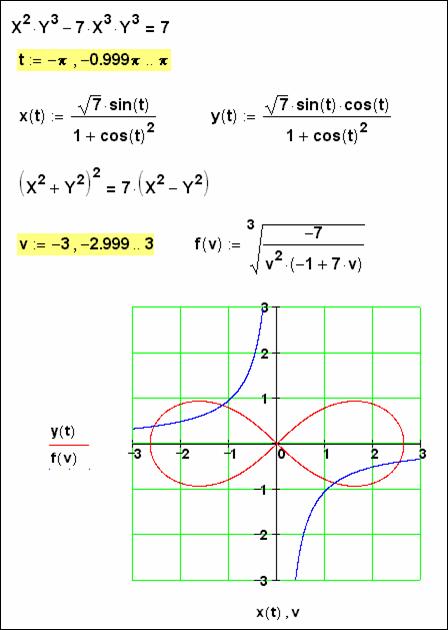
Корреспондент из Канады (jmgiraud@infoteck.dr.qc.ca) прислал графическое решение нашей системы двух алгебраических уравнений (см. рис. 2) через параметрическое представление лемнискаты Бернулли:

Решение проблемы «Кружево» в Maple

---

[1] В слово «необычный» вложен следующий смысл. В среде Mathcad есть семь кнопок, нажатие на которые создает на экране дисплея заготовки семи типов графиков: декартов график, полярный график, поверхность, линии уровня, векторное поле, график рассеяния (трехмерный декартов график) и трехмерная столбчатая диаграмма. Если «графическая» задумка пользователя не укладывается в рамки «великолепной семерки Mathcad» (см. одноименную главу из книги), то он (пользователь) может либо попытаться поискать специализированный пакет научной и деловой графики (Axum – http://www.mathsoft.com/Axum, например), либо все-таки исхитрившись построить необычные графические объекты – см. рис. 1.

[2] Оператор символьной математики solve выдает ответ в виде матрицы, число строк которой равно числу корней системы, а число столбцов – числу ее неизвестных. Оператор float, работающий на рис. 2 в «спарке» с оператором solve, побуждает Mathcad выдавать ответ не в аналитическом виде (он часто бывает очень громоздким и ничего не дает ни уму, ни сердцу), а в виде десятичной дроби с плавающей (float) точкой. Ключ 5 справа от слова float – это число значащих цифр в ответе. Без ключа выдается 20 знаков, а максимальное их количество – 250. (Команда Solve из меню Symbolic может выдать решение с 4000 знаками, но она годится только для решения одиночных уравнений, а не систем).

[3] Хорошее правило: нужно начинать решать задачу с ее аналитического анализа.

[4] Еще одно решение проблемы – использование параметрической формы записи системы: x:=x(t) y:=y(t).

[5] Вернее, запоминается точка, по обе тороны которой одна из функций имеет разный знак. Это может быть и корнем и… точкой разрыва. Так построение графика функции 1/x+1/y=0 по описанной методике даст три линии: x=0, y=0 и y=-x, из которых только последняя будет исхомым решением – графиком функции 1/x+1/y=0.

[6] y(x) – это имя переменной, а не функции. Читатель, не верь глазам своим: в среде Mathcad возможны имена переменных со скобками, что недопустимо традиционных языках программирования. В биологии есть явление «мимикрия», когда одно живое существо притворяется не тем, что оно есть на самом деле! Богомол, например, «косит» под сучек, говоря языком современной молодежи. Наша переменная y(x), вернее не переменная, а вектор принимает вид функции (мимикрирует). Это сделано для того, чтобы маркировка графика на рис. 4 выглядела естественной.

[7] Лемниската – «увитая лентами».

[8] Туман (Fog), кстати говоря – это одно из средств повышения объемности трехмерных графиков. Так, на рис. 1, можно видеть еще один «шедевр» автора – «ежик», пардон, мост (bridge) в тумане. Два других инструмента повышения объемности графиков – это перспектива и освещение. Перспектива наряду с туманом была использована при строительстве моста (bridge.mcd): полотно проезжей части вдали сужается (Марк Твен говорил, что многие составные немецкие слова так длинны, что их нужно писать, придерживаясь законов перспективы). Освещение (lighting) графиков можно увидеть на семи «шедеврах» нашей виртуальной галереи (рис. 1): linked.mcd (сцепление двух бубликов-торов), klein.mcd (односторонняя бутылка – объемный аналог ленты Мебиуса), sphere lightind (освещенная сфера – здесь без света от трех источников не обойтись: шар превратился бы в плоский блин), узлы (roteght.mcd и knots.mcd – интересно, можно ли визуализировать гордиев узел, упоминавшийся в статье) и orbital.mcd (это уже не рисунок, а анимация полета Шатла вокруг Земли).

¹Согласно древнегреческой легенде запутанный узел, которым фригийский царь Гордий привязал ярмо к дышлу телеги. Предсказание оракула гласило, что развязавший узел получит господство над миром. По преданию, Александр Македонский в 334 году до РХ в ответ на предложение распутать узел разрубил его мечом. Отсюда «разрубить гордиев узел» – принять быстрое и смелое решение запутанного и сложного вопроса. Насколько наше графическое решение уравнения f(x,y) «быстро и смело», а главное, эффективно и правильно – судить читателям.

[9] Кроме того, в программе на рис. 5 переменные были «англизированы», т.к. программа готовилась к публикации в форуме Collaboratory.

[10] На рис. 5 с помощью недокументированной встроенной Mathcad-функции time зафиксировано время счета – время генерации двух векторов (в них по 28828 элементов) – 124 секунды (Pentium II, 233 МГц). Программы, показанные на рис. 4 и 5, можно оптимизировать по скорости работы. В частности, сильно тормозит работу то, что внутри двойного цикла с параметром (for x … for y…) дважды вычисляется значение анализируемой функции (в точке x, y и в точке x, y+dy: сверху и снизу от предполагаемого корня), хотя это можно делать один раз, используя при этом результат предыдущего вычисления. Изменяя программу в этом направлении, мы ускорим ее работу, но сделаем более сложной для понимания читателями.