Колумбово
яйцо и трехмерная графика Mathcad
В.Очков
«Всеобщая история, обработанная «Сатириконом»[1]», так описывает событие, связанное с клумбовым яйцом: «…во время диспута с учеными Колумб, в доказательство шарообразной формы земли раздавил на глазах присутствующих – без всяких приспособлений – куриное яйцо. Все ахнули и поверили Колумбу».
«Серьезная» же этимология выражения «колумбово яйцо» такая. Многие пытались вертикально поставить куриное яйцо, раскручивая его или подсовывая под него невидимые подпорки… Колумб же стукнул яйцом по столу, слегка надломил скорлупу и поставил яйцо вертикально. Так ли это было и было ли вообще, судить трудно, но выражение «колумбово яйцо» означает неординарное и несколько грубоватое решение какой-либо застарелой проблемы[2].
С колумбовым яйцом автор неожиданно столкнулся, работая в Internet.
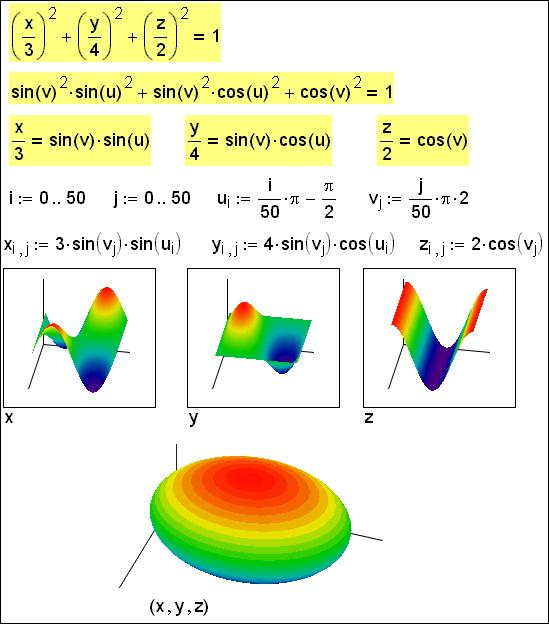
На форуме Collaboratory[3] появился вопрос: «Как построить в среде Mathcad эллипсоид, описываемый уравнением x2/9+y2/16+z2/4=1?». Тут же участники форума стали «раскручивать яйцо, подсовывать под него невидимые подпорки…». Каноническое («с подпорками») решение этой задачи выглядит так (рисунок 1):
Рисунок 1. "Параметрический" эллипсоид
Рассказывают
такую историю. Воздушный шар вырвался из облаков. Летящие увидели на земле
человека и закричали: «Где мы находимся?!». «Вы находитесь в корзине воздушного
шара», — таков был ответ. Его дал математик. Только от математика можно
услышать совершенно точный и совершенно бесполезный ответ[4].
Решение, показанное на рисунке 1, также отличается абсолютной точностью и… абсолютной бесполезностью. Ведь, спрашивающий о построении эллипсоида интересовался, конечно, не конкретным эллипсоидом, а общей методикой построения произвольной фигуры в среде Mathcad. Это типичная «математическая» ситуация: ответ на конкретный вопрос «затуманивается» хитрой методикой его поиска.
Яйцеобразная форма нашего эллипсоида заставляет вспомнить о лаврах Колумба, но не как первооткрывателя Америки[5], а как человека, решившего проблему одноименного яйца[6]. Посмотрим, как можно по-колумбовски упростить решение нашей задачи.
Первое «колумбово» решение задачи об эллипсоиде сводится к построению двух поверхностей, аналитическое описание которых получается при поиске корней уравнение эллипсоида относительно переменной z:
Рисунок 2. Эллипсоид, склеенный из двух половинок
У эллипсоида на рисунке 2 два недостатка – внешний и внутренний:
· внешний недостаток – на графике видно место «склейки» двух поверхностей, образующих эллипсоид
· внутренний недостаток – данную методику не всегда удается перенести на замкнутую поверхность иной формы.
Второе «колумбово» решение задачи об эллипсоиде можно получить, если строить не сам эллипсоид (замкнутую поверхность 2-го порядка), а… геометрическое тело, ограниченное эллипсоидом.
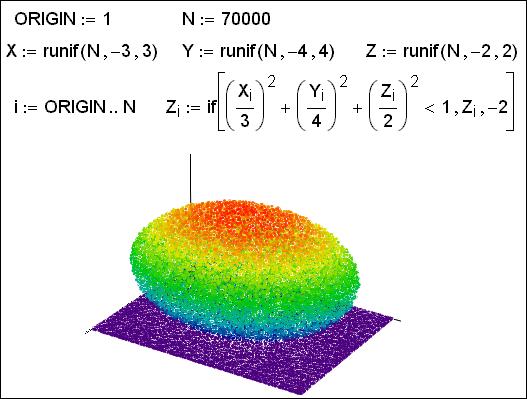
Рисунок 3. «Точечный» эллипсоид
На рисунке 3 показана совокупность точек с координатами X, Y и Z, которые оказались внутри эллипсоида. Остальные точки «упали на пол» – их Z-координата равна минус 2. Детально эта методика «ваяния на компьютере» описана в книге «Mathcad для студентов и инженеров». Эллипсоид у нас получился как бы собранный их точек[7], но зато данная «точечная» методика, годится для любой замкнутой поверхности.
Так на рисунке 4 можно увидеть, например, «объемную» лемнискату Бернулли.
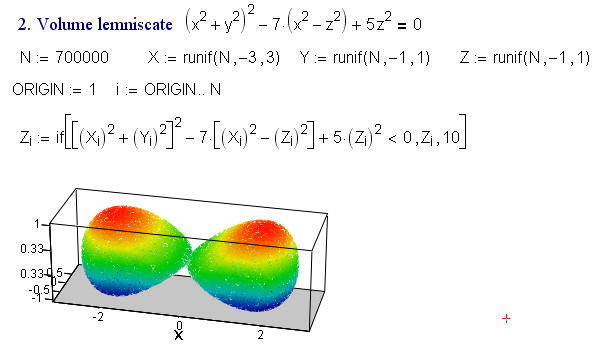
Рисунок 4. «Объемная» лемниската Бернулли
На рис. 4 лишние точки не упали на «на пол» (как на рис. 3), а «ушли в небо»: их z-координата равна 10, а график отформатирован так (z = -1…+1), что точек не видно.
На рис. 5 показано построение «объемной» лемнискаты Бернулли в среде Maple.
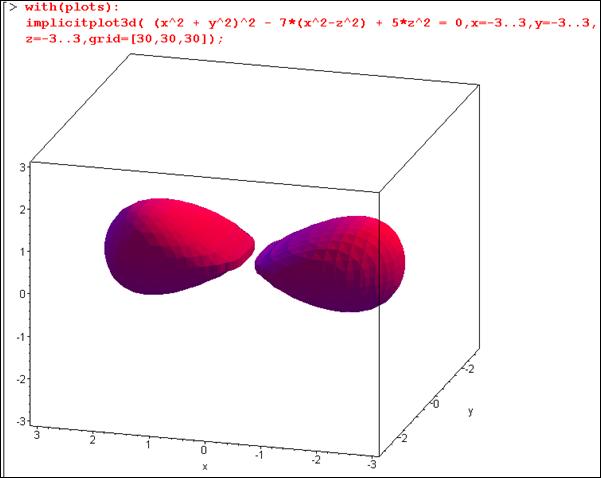
Рисунок 5. «Объемная» лемниската Бернулли в среде Maple
Резюме:
· В статье «История одного шедевра» рассказывалось, как можно в среде Mathcad строить сложные плоские линии. Настоящая статья переводит задачу из плоскости в пространство.
· Автор ждет от читателей интересных объемных фигур. Здесь самое главное – придумать замысловатое равенство или неравенство, связывающее x, y и z.
· Продолжение темы в статье (в главе книги) «Ваяние на компьютере» – http://twt.mpei.ac.ru/ochkov/mc8Pro.book/3_text.htm#_Toc471720706