Путешествие окружности в
треугольнике, а треугольника в ложбине.
А также: какая польза от теорем?
Cразу
без вступлений «берем быка за рога».
Задача: дан треугольник (декартовы
координаты трех его вершин х1-y1, x2-y2 и x3-y3) – найти параметры вписанного в этот треугольник окружности:
ее радиус r
и декартовы
координаты центра (xr и yr: см. рис. 1).
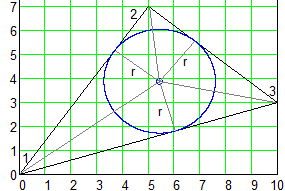
Рис.
1. Задача об окружности, вписанной в треугольник
Можно попытаться поискать в
справочниках или интернете готовые формулы или алгоритмы, по которым рассчитываются
значения искомых переменных r,
xr и yr по значениям заданных переменных х1, y1, x2, y2, x3 и y3. Всех трех готовых формул для трех переменных r, xr и yr ни в справочниках, ни в
интернете найти не удалось (их и быть не может, вернее, пока не может: читаем
дальше). Там можно найти только одну, но очень изящную формулу, по которой
рассчитывается радиус вписанной в треугольник окружности в зависимости от его
площади (S)
и полупериметра (p[1]) или в зависимости от длин
сторон треугольника (a, b, c) и полупериметра (просто площадь
треугольника выражена формулой Герона 
, которую изучают в школе):
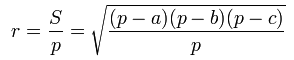
Величины S,
p, a, b, и c
нужно будет
рассчитывать по другим формулам, которые опять же нужно где-то искать или
выводить самому. Длины сторон треугольника можно, например, вычислить по
значениям декартовых координат вершин с привлечением теоремы Пифагора – см. рис. 3.
Рис.
2. Расчет радиуса окружности, вписанной в треугольник
Рисунок 2 – это протокол
расчета радиуса вписанной в треугольник окружности, выполненный в среде Mathcad [1]. Координаты вершин
треугольника измеряются в метрах. Это покоробит многих «чистых» математиков.
Они скажут, причем тут единицы длины[2]?!
Почему здесь именно метры, а не сантиметры, километры или даже футы с дюймами?!
А вот почему. Ввод в расчет единиц измерения позволяет вести контроль
размерностей и выявлять возможные ошибки при вводе формул. Забыл человек,
например, возвести переменную в квадрат или по ошибке возвел ее в куб. Расчет
без метров эту оплошность пропустит, а если ввести размерные величины, то такая
ошибка сразу будет отмечена [2].
При решении задачи о
треугольнике, вписанном в окружность, можно поступить так, как было описано в [3]
– проанализировать задачу, составить систему трех нелинейных алгебраических
уравнений, описывающих положение окружности в треугольнике, и решить ее на
компьютере аналитически (символьно – см. рис. 3) или численно (приближенно – см.
рис. 4). Раньше такую «лобовую атаку» на задачу не делали по понятным причинам
– не было доступных компьютерных средств решения систем нелинейных
алгебраических уравнений. Теперь же – другое дело! Данные три уравнения получаются,
если исходный треугольник разбить на шесть прямоугольных треугольников (см. рис. 1). В каждом из них одна
из вершин упирается в центр окружности, а один из катетов является радиусом
окружности. Гипотенузами этих прямоугольных треугольников будут отрезки прямых,
соединяющих искомый центр окружности с вершинами данного
треугольник. Наши уравнения, показанные на рисунках 2 и 3, фиксируют то
положение, что длины сторон исходного треугольника – это суммы длин пар катетов
смежных прямоугольных треугольников.
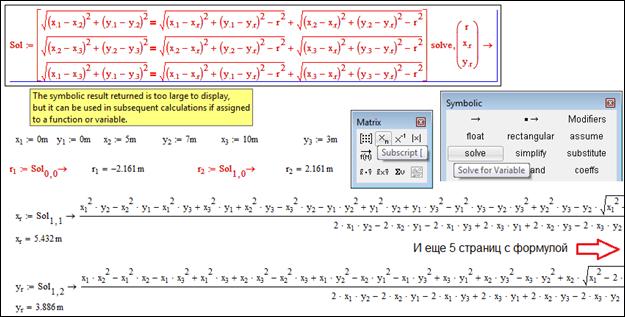
Рис.
3. Аналитическое решение задачи об окружности, вписанной в треугольник
На рис. 3 показано
использование в среде Mathcad символьного
(аналитического) оператора solve
при поиске формул для переменных r, хг и уг, подстановка которых в исходные
уравнения превращают их строго в тождества. Mathcad решил поставленную
задачу, но не смог выдать «на печать» очень объемный ответ – матрицу с двумя
столбцами (два решения системы) и тремя строками (три неизвестных системы). Сообщение об этой ошибке
«вывалилось» из «покрасневшего» оператора solve. Мы вывели «на печать» только малые
части формул для хг и уг. Формулу для r пакет Mathcad «на печать» выдать так и не
смог. Эти формулы можно попытаться упростить, но они все равно останутся
слишком объемными. Поэтому-то их и нет в справочниках или интернете.
По трем формулам
(двум видимым и одной невидимой – см. рис. 3) были
подсчитаны значения искомых переменных r, xr и yr при заданных ранее значениях
координат вершин треугольника.
Рис.
4. Численное решение задачи об окружности, вписанной в треугольник
На рисунке 4 показано
численное решение нашей системы трех
нелинейных уравнений. Для этого записываются исходные данные (координаты вершин
треугольника), вводится ключевое слово Given (Дано), и задаются значения
первого предположения решения. Функция Find (Найти) начинает по особому
алгоритму менять значения своих аргументов (неизвестных системы r, xr и yг) так, чтобы прийти в конце концов к решению – найти
значения этих неизвестных, подстановка которых в исходные уравнения превращает
их в тождества. Вернее, почти
(примерно, приближенно) в тождества:
правые и левые части уравнений должны отличаться на наперед заданное число CTOL. По умолчанию CTOL = 10-3, а единицы измерения при этом
равны базовыми СИ – метры в нашем случае. Т.е. наша геометрическая задача
решена с точностью до миллиметра. Если б мы наш треугольник и окружность
измеряли не в метрах, а в сантиметрах (что более естественно – вспомним, как мы
вычерчиваем геометрические фигуры в линованной тетрадке по математике), то
ответ был бы слишком грубым. Тут нужно было бы менять значение системной
переменной CTOL
на значение 10-7, например.
А по какому алгоритму функция Find «толкает» значения неизвестных от
начального приближения, заданного пользователем, к решению?! Можно узнать
название этого алгоритма (метода – см. рис. 5),
нажатием правой кнопки мыши на слове Find и затем найти информацию по конкретному
методу в том же интернете. А можно поступить несколько иначе.
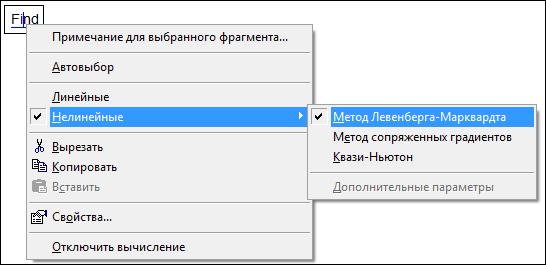
Рис.
5. Выбор метода решения системы уравнений в среде Mathcad 15
Пакет Mathcad 15, в среде которого численно
решалась задача (рис. 4), имеет возможность записи промежуточных значений искомых
величин при реализации тех или иных встроенных инструментов численного решения
задач. В нашем случае можно вспомнить крылатую фразу и
сказать: «Цель ничто – движение всё!». Нас особо не интересует место «вписывания» окружности в
треугольник, но как окружность туда
«закатывается численно» – вот это нам интересно.
На рис. 6 показана
траектория движения центра нашей окружности от точки начального предположения (х = 10 m, y = 10 m) до «цели» – до решения (x = 5.432 m, y = 3.886 m). Мы специально задали пакету Mathcad довольно трудное задание –
поместили точку начального предположения вне треугольника, чтобы посмотреть,
как пакет «будет идти к цели»: «Много ты компьютер о себе воображаешь –
посмотрим, проглотишь ли ты вот это!». А
нужно было бы, конечно, задать значения первого предположения вблизи решения –
где-то в центре исходного треугольника. Но, повторяем «Цель ничто – движение
всё!».
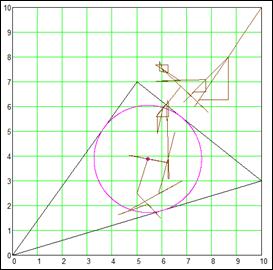
Рис.
6. Траектория движения центра окружности в треугольник
Интересно просмотреть
это движение окружности в анимации, инструменты создания которой есть в Mathcad 15 [4]. На рис. 7 показан
начальный кадр этой анимации (n=0): окружность (видна только ее
дуга-четверть) с радиусом 1 m находится в точке х = 10 m, y = 10 m. Затем (первые 94 кадра
анимации) окружность срывается с места и ударяется о ближайшую сторону
треугольника (рис. 8), подскакивает и ударяется снова.
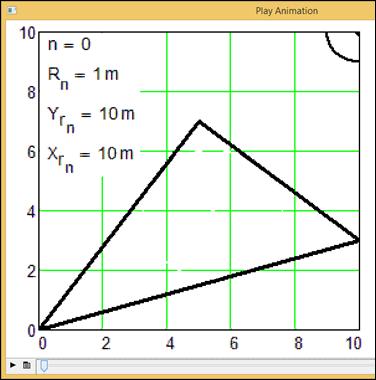
Рис.
7. Начальный кадр анимации движения окружности в треугольник
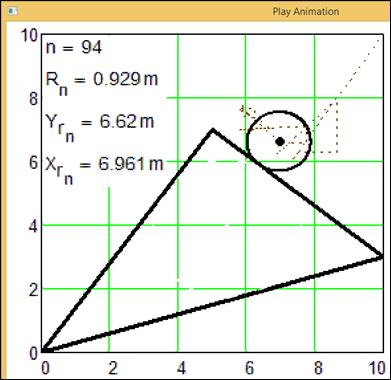
Рис.
8. 94-й кадр анимации движения окружности в треугольник
Далее
окружность «катается» по этой стороне треугольника, пытаясь проникнуть в него
(рис. 8). Эти попытки оказываются безуспешны. Тогда наша окружность начинает уменьшаться
почти до точки (рис. 9), находит некую «дырочку» в треугольнике и проникает в
него (рис. 10).
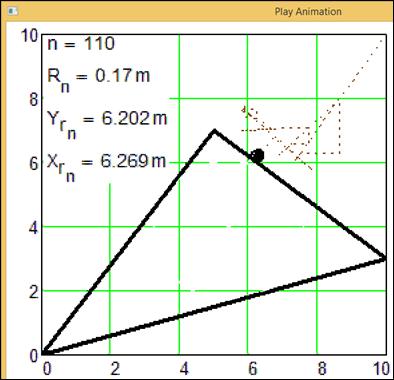
Рис.
9. 110-й кадр анимации движения окружности в треугольник
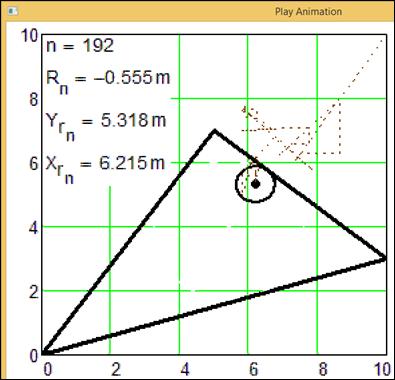
Рис.
10. 192-й кадр анимации движения окружности в треугольник
Затем окружность начинает
«биться» внутри треугольника (рис. 11), пока не найдет в нем свое место –
решение задачи (рис. 12).
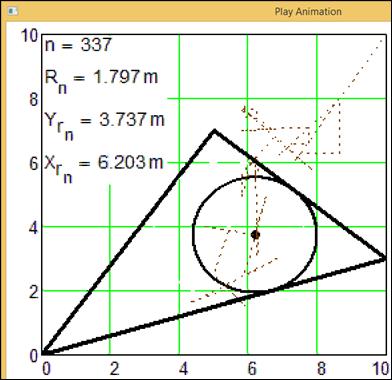
Рис.
11. 337-й кадр анимации движения окружности в треугольник
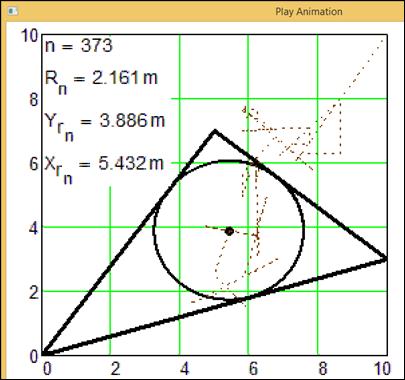
Рис.
12. Финальный кадр анимации движения окружности в треугольник
Такое «живое» поведение
окружности при «численном» ее вписывании в треугольник, отображенном на рис. 7
– 12, видно только при хорошем пространственном воображении. Но можно рисунки с
кадрами анимации вырезать из журнала, сшить их в блокнот, быстро перелистывать
его, перегнув и зажав пальцами страницы и отпуская их[3].
Такие книжки-игрушки была очень популярны до изобретения кино. Данная анимация
(рис. 7-12) на сайте PlanetPTC
имеет номер 3972[4].
Как можно выводить промежуточные
данные при запуске встроенных в Mathcad 15 инструментов численного
решения задачи?
Для этого в среде Mathcad есть три инструмента: встроенная
функция trace,
режим работы Toggle
Debugging
(Режим отладки) и
окно Trace
Window, куда
заносятся промежуточные данные. Все они показаны на рис. 13.
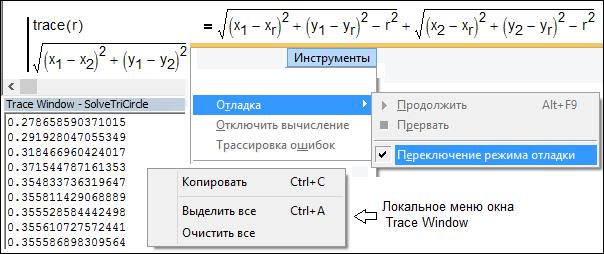
Рис.
13. Инструменты вывода промежуточных результатов численного поиска решения
Функция trace при этом должна быть вставлена в
одно из алгебраических уравнений (см. верхний левый
угол на рис. 13). Аргументами функции trace будут поочередно радиус окружности (как на рис. 13)
и координаты центра, начальные, промежуточные и конечные значения которых будут
автоматически заноситься в окно Trace Window (левый нижний угол рис. 13),
если включен режим отладки (правая часть рис. 13).
На сайте PlanetPTC
можно увидеть анимацию (номер 5015) численного решения «обратной» задачи – задачи
об окружности, описанной в треугольник. Окружность срывается с места в центр
треугольника почти к решению, а затем «в сомнениях» (опять живой организм!)
начинает рыскать в нем, отыскивая решение, вернее, проверяя его правильность.
Таким образом
в окне Trace
Window
можно поочередно сгенерировать
три вектора по r,
xr и yr,
перенести их в расчет и создать по ним анимацию движения окружности от точки
первого предположения до конечной точки. При этом можно менять начальные размер
и положение окружности, а также метод численного решения задачи и точность поиска
корня алгебраического уравнения. Так можно «снимать довольно увлекательное
кино», т.е. заниматься своего рода искусством [5].
Ну, а если особо не увлекаться
съемками кино, а решать задачу о вписывании окружности в треугольник, то нам
понадобятся три теоремы.
Теорема 1. Все три биссектрисы
треугольника пересекаются в одной точке.
Теорема 2. Центр вписанной в
треугольник окружности лежит в точке пересечения биссектрис.
Теорема 3. Биссектриса угла треугольника
делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Кстати, в предыдущих расчетах мы
опирались еще на одну важнейшую теорему: радиус окружности, проведенный в точку
касания, перпендикулярен касательной. Именно поэтому мы рассматривали шесть
прямоугольных треугольников и составляли для них нелинейную систему уравнений.
Итак, опираясь на три теоремы,
наметим план решения поставленной задачи. Нам достаточно найти точку
пересечения лишь двух каких-либо биссектрис (теорема 1). Для этого нам
понадобятся уравнения этих биссектрис. Уравнение прямой (биссектрисы) получим,
зная две точки, лежащие на этой прямой.
Мы исходим из того, что длины
сторон исходного треугольника уже найдены. Обозначим 
длину стороны 
, 
длину стороны 
и 
длину стороны 
(см.
рис. 1). Пусть 
– биссектриса угла 
, а точка 
лежит на стороне . Аналогично 
– биссектриса угла 
, а точка 
лежит на стороне . Тогда (теорема 3) имеем соотношения 
и 
.
Если известны две точки плоскости
,
то координаты точки 
,
которая делит отрезок 
в
отношении 
,
выражаются формулами:
.
Используя указанные формулы,
легко вычисляем координаты точек 
и 
.
Уравнение
прямой в общем случае имеет вид 
. Но поскольку в начале координат находится вершина
, то искомые биссектрисыи через начало координат
не проходят, а поэтому уравнение каждой биссектрисы будем искать в упрощенном
виде 
. Искомые коэффициенты получатся из системы, полученной при
подстановке в уравнение прямой координат двух точек, лежащих на этой прямой. Так, уравнение для биссектрисы будет иметь вид 
, где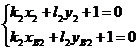 
, а для биссектрисы будет иметь вид 
, где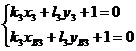 
. Осталось найти точку 
пересечения этих
биссектрис, поскольку (теорема 2) она и является центром окружности. Координаты
, таким образом, находятся из системы шести линейных
уравнений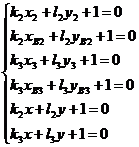 
, в которой числа 
известны по условию, а
числа 
уже найдены.
Ух! Вернемся к играм с
нелинейными уравнениями.
Система алгебраических уравнений,
показанная на рис. 3 и 4, как мы уже отметили, имеет два решения с положительным
значением r
и таким же, но отрицательным значением r. На рис. 14 показана другая система
двух алгебраических уравнений – уравнения эллипса и уравнения лемнискаты
Бернулли, которая имеет уже шесть действительных корней. Вокруг этих замкнутых
кривых и точек их пересечения (корни системы двух уравнений) в анимации вращается
по окружности точка первого предположения. Другая точка (текущее решение
системы уравнений) перескакивает с одного места на другое.
Эта авторская анимация на сайте PlanetPTC имеет номер 2418. Она показывает,
как точка первого предположения влияет на решение системы – на выбор того или
иного корня. Иногда вместо термина «первое предположение»,
очень важного при использовании численных методов решения задач, используют
термин «начальное приближение», что
не совсем верно, и анимация, показанная на рис. 13, доказывает это: очень часто
решение – это не точка, ближайшая к исходной, а совсем
другая, а в ряде случаев – даже самая дальняя. Все зависит от системы уравнений
и метода, мримененного для ее численного решения.
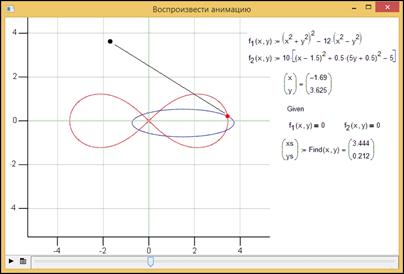
Рис.
14.
А теперь посмотрим, как уже не
окружность, треугольник может вести себя как живое существо – переползать куда-то.
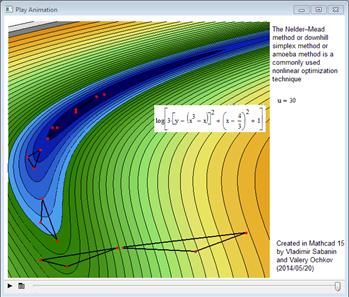
Рис.
15.
Наблюдая в анимации движение
окружности, мы видим, что она ведет себя как некий живой организм, забивающийся в свою треугольную «норку». Тут впору
вспомнить, что некоторые численные методы решения задач имеют «животные»
названия. Так один из методов поиска минимума функции называется «Амеба». Его
кадры анимации (номера 4984, 4980 и 4979) показана на рис. 15 (анимация № 4984):
футуристическая треугольная амеба переваливаясь с боку на бок, ползет в ложбину
(минимум функции двух аргументов), уменьшаясь при этом в размерах (сжимаясь),
пока не найдет эту точку минимума.
Можно найти в Интернете описание
этого метода оптимизации (другие его названия – метод Метод
Нелдера — Мида, метод
деформируемого многогранника, симплекс-метод) и понять его суть. Метод довольно
сложен и в описании, и в реализации, но эффективен: точка минимума находится
быстро (за малое число ходов) и довольно точно. Если у анализируемой функции не
две, а три переменные, то треугольник заменяется тетраэдром и т.д.
На рис. 16 показан более простой,
но менее быстрый авторский метод оптимизации, который условно можно назвать
«Два шага» (номер анимации 1460).
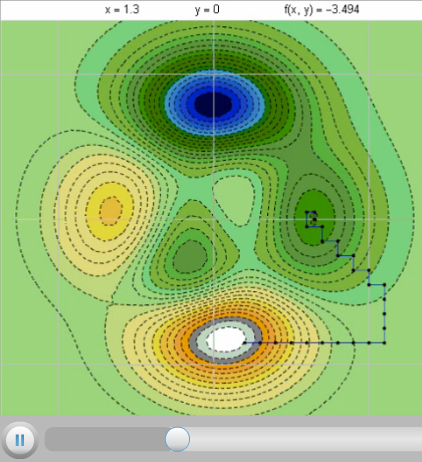
Рис.
16.
Программа, повторяем, довольно проста – у авторов больше времени ушло на поиск ей названия, чем на ее написание. Можно было бы, конечно, тут применить стандартный метод градиентного спуска, при котором шаги делаются по направлению градиента (при поиске максимума) или минус градиента (при поиске минимума), но я искал именно самую простую в реализации программу, особо не думая о ее скорости. Программа названа «Два шага – Two step». Есть такой бальный танец. Один персонаж фильма «Свадьба в Малиновке» называл его «В ту степь». Программа при поиске минимума делает два шага от очередной точки приближения (от «печки», если опять же вспомнить танцы) и переносит опорную точку туда, где значение оптимизируемой функции минимально. Эти два шага длинной X делаются по всем координатам (их число L) в отрицательном (-D) и положительном (D) в направлениях. По мере приближения к минимуму шаги укорачиваются. «Танец» повторяется до тех пор, пока шаг не станет короче заданного значения погрешности (D<СTOL – см. рис. 17).
Рис. 17. Mathcad-программа «Два шага»
Программа «выводит» на печать не только финальную точку, а весь путь к этой точке (матрица М), который несложно отобразить на графике и анимировать.
В программе интересен не сам алгоритм, а след, оставляемый программой на плоскости X-Y («в степи») при оптимизации функции двух переменных – см. рис. 18 и 19.
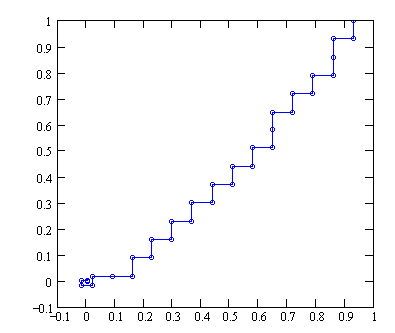
Рис. 18. Начальные шаги приближения к минимуму
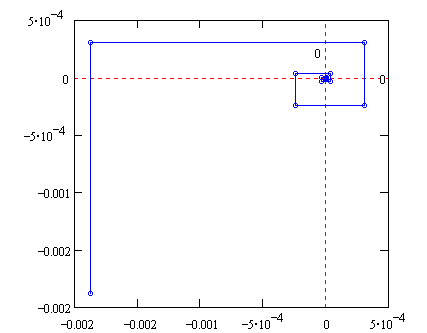
Рис. 19. Конечные шаги приближения к минимуму
Форма следа программы «Тустеп» позволила дать ей и другие названия. У многих народов считается, что чем больше у человека имен, тем больше у него небесных покровителей. Это, наверное, можно отнести и к программам.
Если наполнить ванну водой, бросить в нее, к примеру, перышко и выдернуть пробку, то перышко сначала будет более-менее спокойно двигаться к сливной дырке, а потом закрутится в водовороте. Совсем как на наших рис. 18 и 19: при начальных шагах приближения (рис. 18) промежуточные точки спокойно дрейфуют к минимуму, а затем «закручиваются в вихре танца» (рис. 19), который позволяет называть данный метод оптимизации не только «Тустеп», но и «Вальс». Но если быть совсем точным, то его следует именовать также и методом наискорейшего спуска воды. И вот почему.
Вода в ванне или в каком-либо ином сосуде с дыркой на дне всегда закручивается в одну сторону. Даже если воду раскрутить рукой в другом направлении, то, преодолев насилие, она вернет свою природную закрутку. Это связано с силой Кориолиса, которая в свою очередь зависит от вращения Земли вокруг своей оси. В северном полушарии вода закручивается по часовой стрелке, в южном – против, на экваторе – сливается без вихрей (а на полюсах – совсем не течет: замерзает: шутка!). Это явление основательно изучалось в Alma Mater авторов статьи (в Московском энергетическом институте) применительно к барабанным паровым котлам. Дело в том, что вода из барабана котла, поступая в опускные трубы, а затем в подъемные трубы, расположенные в топке котла, может закручиваться и захватывать вследствие этого большие порции водяного пара. Это может приводить к ухудшению теплообмена и даже к авариям – разрывам паровых труб. Подробнее об этом здесь: http://twt.mpei.ru/ochkov/KotelVikhr.html.
Для проверки этой гипотезы авторы переслали по Интернету файл с программой оптимизации коллеге в Австралию (чем черт не шутит) и к полному своему удивлению, переходящему в удовлетворение, узнали, что след поиска минимума в южном полушарии закручивается против часовой стрелки. «Австралийский» след оптимизации из-за экономии места здесь не приводится. Но его можно увидеть, посмотрев на рис. 18 и 19 через зеркало.
Причина иной закрутки следа поиска минимума южнее экватора, конечно, не в воде, хотя сила Кориолиса здесь присутствует: при пересылке файла в Австралию в текст программы вкралось маленькое изменение. Вместо строки for X Î -D, D появилась другая – for X Î D, -D. На поиск минимума это не повлияло (перебор координат оптимизируемой функции ведется всего лишь с другого конца), но, тем не менее, след стал закручиваться по-иному. А виной тому все та же сила Кориолиса, заставляющая жесткие диски серверов и маршрутизаторов в южном полушарии Земли вращаться несколько иначе, чем в северном полушарии. Отсюда и незначительные сбои при пересечении файлами экватора. Их выловить довольно трудно, т.к. при контрольной обратной пересылке файла ошибка исправляется по принципу минус на минус дает плюс.
Литература:
1. Очков В. Ф. Mathcad 14 для студентов, инженеров и конструкторов. — СПб.: БХВ-Петербург, 2007. — 368 с. URL: http://twt.mpei.ac.ru/ochkov/Mathcad_14/RusIndex.html
2. Очков В. Ф. Физические и экономические величины в Mathcad и Maple (Серия "Диалог с компьютером"). — М.: Финансы и статистика, 2002. — 192 с. URL: http://twt.mpei.ac.ru/ochkov/Units/Forword_book.htm
3. Очков
В. Ф. Преподавание математики и математические пакеты // Открытое
образование. — 2013. — № 2. — С. 23–34. URL: http://twt.mpei.ac.ru/ochkov/Mathcad-15/OchkovMath.pdf
4. Очков
В. Ф. Живые кинематические схемы в Mathcad // Открытое образование, №3, 2013. С. 27-33. URL:
http://twt.mpei.ac.ru/ochkov/Mathcad-15/kinematic.html
5. Очков В. Ф. Решение алгебраических уравнений и систем или Ван Гог в среде Mathcad // КомпьютерПресс. № 9. 2001. URL: http://twt.mpei.ac.ru/ochkov/Carpet/index.htm
6. Очков В. Ф. Программирование и сила Кориолиса или Необычайное приключение файла в Интернете // КомпьюТерра. № 13. 1997. URL: http://twt.mpei.ac.ru/ochkov/Koriolis.htm
7. Б.М. Яворский, А.А. Детлаф «Справочник по физике для инженеров и студентов вузов». М.: Наука, 1977