Что нам стоит мост построить…
(English version)
(Рисунок
моста в галерее фирмы Mathsoft.
Inc, - разработчик
пакета Mathcad)
В. Очков http://twt.mpei.ac.ru/ochkov
В среде Mathcad 2000[1]
появилось около тридцати новых функций (см. статью «Mathcad 2000: первые впечатления» на CD-ROM № 12’
1999). Среди этих функций особо выделяется функция odesolve. Ее уникальность в том, что она возвращает не
скаляр, вектор или матрицу, как все остальные «нормальные» встроенные функции Mathcad,
а функцию одного аргумента, являющуюся решением (to solve –
решать) обыкновенного дифференциального уравнения (ode – ordinary differential equation).
До 2000 версии в среде Mathcad
эта задача решалась довольно неуклюже. Одиннадцать встроенных функций (Bulstoer, bulstoer, bvalfit, Rkadapt, rkadapt, rkfixed, sbval, Stiffb, stiffb, Stiffr и stiffr) возвращали не решение обыкновенного дифференциального уравнения
(функцию, подстановка которой и ее производных в исходное дифференциальное
уравнение, превращает его в тождество), а вектор значений искомой функции.
Чтобы все-таки получить искомую функцию приходилось проводить, например,
сплайн-интерполяцию. Функция odesolve –это «шампунь и кондиционер
в одном флаконе»: она объединяет процесс численного решения обыкновенного
дифференциального уравнения (генерация вектора) и интерполяции полученных точек
(формирование функции).
Функция odesolve
вернула процессу решения задачи, если так можно выразиться, ее красоту и
естественность.
В среде Mathcad 2000 обыкновенное
дифференциальное уравнение внешне решается также как и алгебраическое уравнение
– условия задачи «зажимаются» между ключевым словом Given
(дано) и встроенной функцией odesolve (или Find – найти, если говорить об
алгебраическом уравнении). В условия задачи входит само дифференциальное
уравнение и ограничения, сводящие задачу либо к задаче Коши, либо к краевой
задаче.
Проиллюстрируем «красоту» функции odesolve красивой графической интерпретацией ее решения,
рассмотрев «заглавную» задачу: через реку необходимо перекинуть висячий мост,
цепи которого закреплены на краях и в промежутке на двух пилонах. Искомая функция, описывающая провисание цепи (цепная
функция) имеет одну особенность – ее вторая производная равна
(точнее - пропорциональна) самой
функции[2]. Решение в среде Mathcad
2000 Pro этой краевой задачи по обыкновенному дифференциальному уравнению
второго порядка показано на рис. 1.
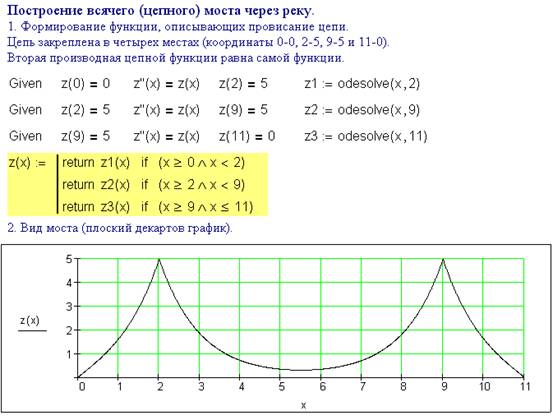
В результате мы сформировали
кусочно-непрерывную функцию Z(x), по которой можно построить плоский декартов график – вид висячего
моста в профиль[3], если так
можно выразиться.
Но мост это сугубо объемная конструкция и
отображать ее нужно объемной (трехмерной) графикой. В среде Mathcad
есть трехмерный аналог декартового графика Scatter Plot –
«график россыпи, рассеяния» (to scatter, по-английски рассыпать, расшвыривать,
разбрасывать). Если декартов график «работает» с двумя векторами, «рассеивая»
их значения[4] на плоскости, то Scatter Plot требует наличие уже трех векторов (у нас это будут Х, Y и Z), рассеивая точки с данными координатами в объеме [5].
Эти точки можно соединить
линиями, ведя их, руководствуясь номером точки (от нулевой точки к первой, от
первой – ко второй и т.д. до последней) либо значениями элементов векторов Х, Y или Z. Кроме того, точки и линии может раскрасить так, чтобы оттенки цвета[6]
менялись опять же в зависимости от номера точки либо от значений элементов
векторов Х, Y или Z.

На рис. 2
наша мостовая цепь, оставаясь плоской (Yi := 0), приобрела объемность в смысле ориентации к
зрителю.

И, наконец, на рис. 3 мы получили изображение висящего моста в
«пол-оборота». Для этого:
·
векторы
Х,Y или Z мы удлинили ровно вдвое: c одного
берега реки тянется цепь (X), затем она поворачивает
назад (reverse(X)[7]); ширина моста равна двум (Yi := 0, Y1i := 2)
·
звенья
цепи, опирающиеся на пилоны, опускаются на землю (Z20 := 0, Z90 := 0);
·
трехмерный
график форматируется особым образом: оси и сетки убираются, цепь раскрашивается
по оси Z, проезжая часть – это закрашенная плоскость X-Y, по
оси Y проводятся три белые линии сетки (разметка
проезжает части); у самой же конструкции повышена объемность за счет
использования перспективы и тумана.
Сейчас компьютер широко используется как
рабочий инструмент художника (интеллектуальная кисть или что-то в этом роде).
Распечатки цветных принтеров оправляются в рамки и выставляются в, так сказать,
реальных и виртуальных компьтерно-художественных салонах (см., например, журнал
«КомпьюАрт»).
Но автору хотелось бы обратить внимание
уважаемых читателей на другое – на проблему эстетического вида не просто
компьютерных рисунков, а листингов
программ и, в частности, на проблему соответствия (или противопоставления)
формы листинга содержанию программы.
Программисты, которым не чуждо образное
мышление, давно уже подметили, что процедуры и функции имеют свое собственное
«лицо», по которому она безошибочно узнается на экране дисплея или на бумаге
принтера. Одна процедура как ухоженная крестьянская лошадка круглая и гладкая –
работает себе спокойно, перекачивая, например, данные из одного формата в
другой. И внешне она неприметна –
взгляд на ней не останавливается. Другая процедура все время норовит
выкинуть какой-нибудь фортель, настолько она неотлаженна (необъезженна). И
своими очертаниями она походит на скакуна, в седле которого сидит герой
многочисленных живописных полотен и скульптур. Третья процедура так и просится,
чтобы ее оправили в раму и повесили на стену, настолько она хороша и закончена,
а главное, ее форма полностью отвечает ее содержанию. Она передает не только мысли, но даже и настроение художника, пардон, программиста, ее создавшего.
Автор далеко не искусствовед и не смеет особо
распространяться на эту тему.
В комментариях к публикуемым компьютерным
рисункам, как правило, подчеркивается, что их авторы – компьютерные художники. В прилагательных к существительным очень
часто таится некая ущербность или по,
крайней мере, двусмысленность: не
просто математика, а «Прикладная математика». Термин компьютерный художник содержит в себе некую двойственность. С одной
стороны, прилагательным «компьютерный» как бы извиняются перед потенциальным
зрителем за эстетику рисунков (см. наш «рисунок» моста). А с другой стороны –
предупреждают о том, что при создании рисунков использовались специфические
инструменты и методы (авангардистские изыски).
Настоящий художник готов работать на чём угодно и чем угодно. Рисунки Анатолия Зверева (художника с трагической
судьбой, какая, увы, часто постигает гениев; недавно в Москве прошла его
выставка), выполненные чуть ли не окурком на обрывке листа бумаги, продаются на
аукционах за большие деньги. Давайте дождемся времен, когда распечатки
принтеров будут выставляться в Лувре, в Эрмитаже или на худой конец продаваться
на художественных аукционах. Последнее вряд ли случится. На аукционах могут
продать дискету, принадлежавшую компьютерному художнику (фетиш – сейчас так
продаются гитары великих музыкантов). Дело в том, что у computer art нет
понятия оригинала и копии[8].
А это может убить даже настоящие шедевры, которые иногда публикуются на
обложках и внутри глянцевых изданий. Пушкин говорил: «Пóшло то, что пошлó в народ». Только самые гениальные
произведения искусства способны выдержать такое испытание хождением в народ.
Они-то и формируют пласт культуры, на котором базируется современная
цивилизация.
Лучший способ охарактеризовать какое-либо явление – тем более в статье с претензией на искусствоведение – это привести классическую цитату. Вот она:
Они сначала нравилися мне
Глазами синими, да белизною,
Да скромностью – а пуще
новизною;
Да, слава богу, скоро
догадался –
Увидел я, что с ними грех и
знаться –
В них жизни нет, все куклы
восковые;
А наши!...
Угадайте, о чем говорил пушкинский Дон Гуан! Да-да –
и о компьютерной анимации, о рисунках, созданных с помощью компьютерной
графики... Скажем мягче (и с надеждой) – о современных образцах этого симбиоза
науки, технологии и искусства. Ведь, в компьютерных рисунках больше чувствуется
несовершенный инструмент (новизна –
парадокс high technology), чем художник.